题目内容
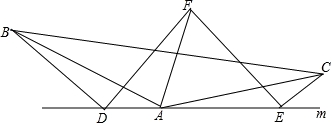
如图,在△ABC中,AB=AC,D、A、E在直线m上,∠ADB=∠AEC=∠BAC.
(1)求证:DE=DB+EC;
(2)若∠BAC=120°,AF平分∠BAC,且AF=AB,连接FD、FE,请判断△DEF的形状,并写出证明过程.
【考点】全等三角形的判定与性质.
【分析】(1)由∠ADB=∠AEC=∠BAC,于是得到∠ADB+∠ABD+∠BAD=∠BAD+∠BAC+∠EAC=180°,推出∠ABD=∠EAC,证得△ABD≌△AEC,根据全等三角形的性质得到BD=AE,然后根据线段的和差即可得到结论;
(2)由等边三角形的性质就可以求出∠BAC=120°,就可以得出△BAD≌△ACE,就有BD=AE,进而得出△BDF≌△AEF,得出DF=EF,∠BFD=∠AFE,进而得出∠DFE=60°,就有△DEF为等边三角形.
【解答】(1)证明:∵∠ADB=∠AEC=∠BAC,
∴∠ADB+∠ABD+∠BAD=∠BAD+∠BAC+∠EAC=180°,
∴∠ABD=∠EAC,
在△ABD与△ACE中,
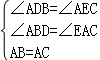 ,
,
∴△ABD≌△AEC,
∴BD=AE,
∵DE=AD+AE,
∴DE=DB+EC;
(2)△DEF为等边三角形
理由:∵△ABF和△ACF均为等边三角形
∴BF=AF=AB=AC=CF,∠BAF=∠CAF=∠ABF=60°,
∴∠BDA=∠AEC=∠BAC=120°,
∴∠DBA+∠DAB=∠CAE+∠DAB=60°,
∴∠DBA=∠CAE.
在△BAD和△ACE中,
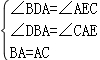 ,
,
∴△ADB≌△CEA(AAS),
∴BD=AE,∠DBA=∠CAE.
∵∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE.
在△BDF和△AEF中,
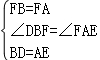 ,
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
【点评】本题考查了全等三角形的判定及性质的运用.等边三角形的判定及性质的运用,等式的性质的运用,解答时证明三角形的全等是关键.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案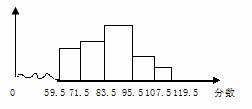 根据(2)中的结论,该区所有参加市模拟考试的学生中,及格人数.优秀人数各约为多少?
根据(2)中的结论,该区所有参加市模拟考试的学生中,及格人数.优秀人数各约为多少?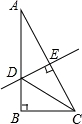




 ﹣a=
﹣a=
 ,且关于x的不等式组
,且关于x的不等式组
 只有4个整数解,那么b的取值范围是 .
只有4个整数解,那么b的取值范围是 .
 B.
B.
 C.
C.