题目内容
12.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x+y=1+a}\\{x+3y=3}\end{array}\right.$的解满足x+y<2.(1)求a的取值范围;
(2)若a=1,方程组的解是等腰三角形的两条边的长,求此等腰三角形的周长.
分析 (1)方程组中的两个方程相加即可求出x+y的值,即可得出关于a的不等式,求出不等式的解集即可;
(2)把a=1代入求出方程组的解,看看是否符合三角形三边关系定理,把符合的求出即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+y=1+a①}\\{x+3y=3②}\end{array}\right.$
①+②得:4x+4y=4+a,
x+y=1+$\frac{1}{4}$a,
∵关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x+y=1+a}\\{x+3y=3}\end{array}\right.$的解满足x+y<2,
∴1+$\frac{1}{4}$a<2,
解得:a<4,
即a的取值范围是a<4;
(2)把a=1代入方程组得:$\left\{\begin{array}{l}{3x+y=2②}\\{x+3y=3②}\end{array}\right.$
①-②×3得:-8y=-7,
y=$\frac{7}{8}$,
①×3-②得:8x=3,
解得:x=$\frac{3}{8}$,
∵$\frac{3}{8}$+$\frac{3}{8}$<$\frac{7}{8}$,
∴等腰三角形的三边只能是$\frac{3}{8}$,$\frac{7}{8}$,$\frac{7}{8}$,
∴此等腰三角形的周长$\frac{3}{8}$+$\frac{7}{8}$+$\frac{7}{8}$=$\frac{17}{8}$.
点评 本题考查了解一元一次不等式,解二元一次方程组,等腰三角形的性质,三角形的三边关系定理的应用,能灵活运用知识点进行计算是解此题的关键,难度适中.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
3.已知(2x-3y+1)2与|4x-3y-1|互为相反数,则x,y的值为( )
| A. | x=-1,y=1 | B. | x=1,y=-1 | C. | x=-1,y=-1 | D. | x=1,y=1 |
4.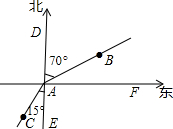 如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A点出发向南偏西15°方向走60m至点C,则∠BAC的度数是( )
如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A点出发向南偏西15°方向走60m至点C,则∠BAC的度数是( )
 如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A点出发向南偏西15°方向走60m至点C,则∠BAC的度数是( )
如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A点出发向南偏西15°方向走60m至点C,则∠BAC的度数是( )| A. | 85° | B. | 160° | C. | 125° | D. | 105° |
1.如果等式(2a-1)a+2=1成立,则a的值可能有( )
| A. | 4个 | B. | 1个 | C. | 2个 | D. | 3个 |
 两个边长分别为2cm和3cm的正方形如图摆放,则图中阴影部分的面积为$\frac{7}{2}$cm2.
两个边长分别为2cm和3cm的正方形如图摆放,则图中阴影部分的面积为$\frac{7}{2}$cm2.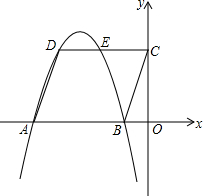 已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.
已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.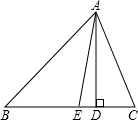 如图,已知△ABC中,AD是BC边上的高,点E在线段BD上,且AE平分∠BAC,若∠B=40°,∠C=78°,则∠EAD=19°.
如图,已知△ABC中,AD是BC边上的高,点E在线段BD上,且AE平分∠BAC,若∠B=40°,∠C=78°,则∠EAD=19°.