题目内容
10．如果最简二次根式$\sqrt{3a-8}$与$\sqrt{17-2a}$可以合并，那么使$\sqrt{4a-2x}$有意义的x的取值范围是x≤10．分析 根据二次根式可合并，可得同类二次根式，根据同类二次根式，可得a的值，根据被开方数是非负数，可得答案．
解答 解：由最简二次根式$\sqrt{3a-8}$与$\sqrt{17-2a}$可以合并，得
3a-8=17-2a．
解得a=5．
由$\sqrt{4a-2x}$有意义，得
20-2x≥0，解得x≤10，
故答案为：x≤10．
点评 本题考查了同类二次根式，利用同类二次根式得出关于a的方程是解题关键．
练习册系列答案
相关题目
菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF=$\sqrt{2}$，BD=2，则菱形ABCD的面积为2$\sqrt{2}$．
5．将方程$\frac{0.1x+0.2}{0.3}$=$\frac{0.02x+0.01}{0.05}$变形为$\frac{x+2}{3}$=$\frac{2x+1}{5}$的理论依据是（ ）
| A． | 合并 | B． | 等式的性质 | C． | 等式的性质2 | D． | 分数的基本性质 |
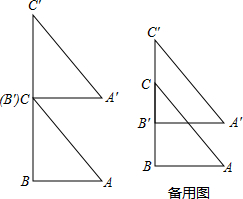如图，已知：Rt△ABC中，∠B=90°，AB=6，BC=8，△A′B′C′≌△ABC，BC与B′C′在同一直线上，点C与点B′重合（如图1），现将△ABC沿射线B′C′以2个单位/秒的速度向上平移，设运动时间为t（s）．