题目内容
14.解不等式组:$\left\{\begin{array}{l}{5x+2>3(x-1)①}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x②}\end{array}\right.$,并把解集在数轴上表示出来.分析 分别求出不等式组中两不等式的解集,确定出不等式组的解集,表示在数轴上即可.
解答 解:$\left\{\begin{array}{l}{5x+2>3(x-1)①}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x②}\end{array}\right.$,
由①得:x>-$\frac{5}{2}$,
由②得:x≤4,
∴不等式组的解集为-$\frac{5}{2}$<x≤4,
点评 此题考查了解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.一个多边形的每一个外角都等于120°,则这个多边形的边数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
9.下列式子一定是二次根式的是( )
| A. | $\sqrt{x-1}$ | B. | $\sqrt{x}$ | C. | $\sqrt{{x}^{2}+2}$ | D. | $\sqrt{{x}^{2}-2}$ |
19.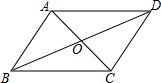 如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
 如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
6.一元二次方程2x2-5x-4=0的二次项系数、一次项系数及常数项分别是( )
| A. | 2,5,-4 | B. | 2,5,4 | C. | 2,-5,-4 | D. | 2,-5,4 |
3. 如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=( )
如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=( )
 如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=( )
如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
4.使式子$\sqrt{x-4}$有意义的条件是( )
| A. | x≥4 | B. | x=4 | C. | x≤4 | D. | x≠4 |
 已知,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为$\frac{1}{2}$,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边长作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边长作正方形A4B4C4A5…,若OA1=2,则正方形AnBnCnAn+1的面积为( )
已知,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为$\frac{1}{2}$,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边长作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边长作正方形A4B4C4A5…,若OA1=2,则正方形AnBnCnAn+1的面积为( )