题目内容
10.某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.若每间的年租金每增加5000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.(1)当每间商铺的年租金定为12万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为285万元?
分析 (1)直接根据题意先求出增加的租金是4个5000,从而计算出租出多少间;
(2)设每间商铺的年租金增加x万元,直接根据收益=租金-各种费用=285万元作为等量关系列方程求解即可.
解答 解:(1)∵(120000-100000)÷5000=4,
∴能租出30-4=26(间).
(2)设每间商铺的年租金增加x万元,则有$\frac{x}{0.5}$间商铺没有出租,出租的商铺需要交$(30-\frac{x}{0.5})×1$万元费用,没出租的商铺需要交$\frac{x}{0.5}×0.5$万元费用;
则:可列方程$(30-\frac{x}{0.5})×(10+x-1)-\frac{x}{0.5}×0.5=285$,
整理得:2x2-11x+15=0,
解得:x=3或x=2.5,
故:每间商铺的年租金应定为12.5万元或13万元;
点评 考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题中的等量关系题目中已经给出,相对降低了难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.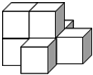 如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )
如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )
 如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )
如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( )| A. | 俯视图 | B. | 主视图 | C. | 俯视图和左视图 | D. | 主视图和俯视图 |
18.一次函数y=ax-a+1(a为常数,且a≠0).
(1)若点$(-\frac{1}{2},3)$在一次函数y=ax-a+1的图象上,求a的值;
(2)当-1≤x≤2时,函数有最大值2,请求出a的值.
(1)若点$(-\frac{1}{2},3)$在一次函数y=ax-a+1的图象上,求a的值;
(2)当-1≤x≤2时,函数有最大值2,请求出a的值.
5.以下问题,不适合用全面调查的是( )
| A. | 了解全班同学每周体育锻炼的时间 | B. | 学校招聘教师,对应聘人员面试 | ||
| C. | 了解重庆庆中小学生每天的零花钱 | D. | 旅客上飞机前的安检 |