题目内容
 ⊙O1和⊙O2相交于B、D两点,⊙O2过⊙O1的圆心,点A、点C分别是⊙O1和⊙O2两段优弧的任意点,若∠C=86°,则∠A的度数为
⊙O1和⊙O2相交于B、D两点,⊙O2过⊙O1的圆心,点A、点C分别是⊙O1和⊙O2两段优弧的任意点,若∠C=86°,则∠A的度数为考点:相交两圆的性质
专题:
分析:连接DO1、BO1,根据圆内接四边形性质求出∠DO1B,根据圆周角定理求出∠A即可.
解答:解:
连接DO1、BO1,
∵D、O1、B、C四点共圆,
∴∠DO1B+∠C=180°,
∵∠C=86°,
∴∠DO1B=180°-86°=94°,
∵∠A=
∠DO1B,
∴∠A=47°,
故答案为:47°.

连接DO1、BO1,
∵D、O1、B、C四点共圆,
∴∠DO1B+∠C=180°,
∵∠C=86°,
∴∠DO1B=180°-86°=94°,
∵∠A=
| 1 |
| 2 |
∴∠A=47°,
故答案为:47°.
点评:本题考查了相交两圆的性质,圆内接四边形的性质,圆周角定理的应用,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题是假命题的是( )
| A、如果两个角是对顶角,那么它们相等 |
| B、同位角相等 |
| C、三角形中相等的边所对的角相等 |
| D、全等直角三角形的两锐角对应相等 |
下列事件是必然事件的是( )
| A、2012年12月31日无锡一定是晴天 |
| B、掷一枚硬币,恰好正面朝上 |
| C、30名同学中至少有两人在同一个月出生 |
| D、打开电视,正在播广告 |
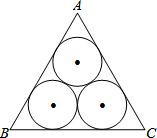 如图,三个半径都为6cm的等圆两两外切,并且△ABC的每一边都与其中两个圆相切,则△ABC的周长为
如图,三个半径都为6cm的等圆两两外切,并且△ABC的每一边都与其中两个圆相切,则△ABC的周长为 如图,在三角形ABC中,∠C=90°,DE⊥AB于点D,DB=BC,如果AC=6,求AE+DE的长度.
如图,在三角形ABC中,∠C=90°,DE⊥AB于点D,DB=BC,如果AC=6,求AE+DE的长度.