题目内容
 如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.
如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.(1)求证:DE是⊙O的切线;
(2)若DE=6,⊙O的半径为10,求BF的长.
考点:切线的判定
专题:
分析:(1)连结OD,若要证明AD平分∠BAC,则问题可转化为证明:∠1=∠2;
(2)作DH⊥AB,可证明△ADH∽△AFB,利用相似三角形的性质:对应边的比值相等即可得到关于BF的比例式,计算即可.
(2)作DH⊥AB,可证明△ADH∽△AFB,利用相似三角形的性质:对应边的比值相等即可得到关于BF的比例式,计算即可.
解答:(1)证明:连结OD,
∵DE是⊙O的切线,
∴OD⊥OE.
又∵DE⊥AC,
∴AE∥OD.
∴∠2=∠ADO,
∵OA=OD,
∴∠1=∠ADO.
∴∠1=∠2,
即AD平分∠ABC;
(2)解:作DH⊥AB于H,
∵∠1=∠2,∠E=90°,
∴DH=DE=6,
∵OD=10,
∴由勾股定理得:OH=8,
∴AH=10+8=18,AB=20,
∵FB是⊙O的切线,
∴∠FBA=90°,
∴DH⊥AB,
∴DH∥BF,
∴△AHD∽△ABF,
∴
=
,
∴
=
,
∴BF=
.

∵DE是⊙O的切线,
∴OD⊥OE.
又∵DE⊥AC,
∴AE∥OD.
∴∠2=∠ADO,
∵OA=OD,
∴∠1=∠ADO.
∴∠1=∠2,
即AD平分∠ABC;
(2)解:作DH⊥AB于H,
∵∠1=∠2,∠E=90°,
∴DH=DE=6,
∵OD=10,
∴由勾股定理得:OH=8,
∴AH=10+8=18,AB=20,
∵FB是⊙O的切线,
∴∠FBA=90°,
∴DH⊥AB,
∴DH∥BF,
∴△AHD∽△ABF,
∴
| DH |
| BF |
| AH |
| AB |
∴
| 6 |
| BF |
| 18 |
| 20 |
∴BF=
| 20 |
| 3 |
点评:本题考查了切线的判定方法,经过半径的外端且垂直于这条半径的直线是圆的切线,注意:辅助线的做法,也考查了相似三角形的性质和判定.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
下列命题中错误的是( )
| A、两组对边分别平行的四边形是平行四边形 |
| B、对角线互相垂直的四边形是菱形 |
| C、一组邻边相等的平行四边形是菱形 |
| D、正方形的对角线相等且互相垂直 |
 如图,是一副普通扑克牌中的13张黑桃牌,将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点小于6的概率为( )
如图,是一副普通扑克牌中的13张黑桃牌,将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点小于6的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列图案中,是中心对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
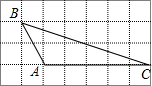 如图,在4×7的正方形网格中,有一个格点三角形ABC,那么∠ABC的正弦值是( )
如图,在4×7的正方形网格中,有一个格点三角形ABC,那么∠ABC的正弦值是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,AD平分∠EAC.
如图,AD平分∠EAC.