题目内容
同时抛掷两枚硬币,正面都朝上的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法
专题:
分析:根据题意,列举同时抛掷两枚质地均匀的硬币出现的情况,可得其情况数目以及出现两个正面朝上数目,由等可能事件的概率,计算可得答案.
解答:解:同时抛掷两枚质地均匀的硬币,出现的情况有(正、正)、(正、反)、(反、正)、(反、反),共4种情况;
出现两个正面朝上即(正、正)有一种情况,
则出现两个正面朝上的概率是
,
故选C.
出现两个正面朝上即(正、正)有一种情况,
则出现两个正面朝上的概率是
| 1 |
| 4 |
故选C.
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
化简
的结果为( )
| 32 |
A、4
| ||
B、4
| ||
C、6
| ||
D、8
|
下列各方程,变形正确的是( )
A、-
| ||||||||
| B、1-2x=x化为3x=-1 | ||||||||
C、
| ||||||||
D、
|
已知a2+b2=6ab且a>b>0,则(
)2的值为( )
| a+b |
| a-b |
| A、0.25 | B、4 | C、2 | D、0.5 |
单项式3a2b2n+1与-3a4-mb7是同类项,则mn等于( )
| A、8 | B、-8 | C、9 | D、-9 |
下列一元二次方程没有实数根的是( )
| A、x2=x |
| B、x2-9=0 |
| C、x2-2x-8=0 |
| D、x2-x+3=0 |
下列计算正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
数学课要学“勾股定理”,小敏在“百度”搜索引擎中输入“勾股定理”,能搜索到与之相关的结果个数约为7160 000,这个数用科学记数法表示为( )
| A、7.16×105 |
| B、7.16×106 |
| C、7.16×107 |
| D、7.16×108 |
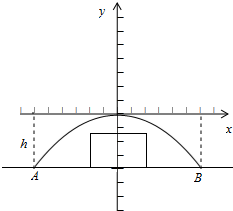 如图所示,有一抛物线形涵洞,其函数表达式为y=ax2(a≠0).涵洞跨度AB=12m,内部高度h=4m.为了安全,卡车经过涵洞时,载货(矩形)最高处与其正上方顶部之间的距离不能小于0.5m.现有一辆运货卡车欲通过涵洞,经测量该车宽4m,载货最高处距地面2.5m.问该车能否通过,为什么?
如图所示,有一抛物线形涵洞,其函数表达式为y=ax2(a≠0).涵洞跨度AB=12m,内部高度h=4m.为了安全,卡车经过涵洞时,载货(矩形)最高处与其正上方顶部之间的距离不能小于0.5m.现有一辆运货卡车欲通过涵洞,经测量该车宽4m,载货最高处距地面2.5m.问该车能否通过,为什么?