题目内容
7.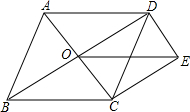 如图,菱形ABCD,对角线AC、BD交于点O,DE∥AC,CE∥BD,求证:OE=BC.
如图,菱形ABCD,对角线AC、BD交于点O,DE∥AC,CE∥BD,求证:OE=BC.
分析 先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明四边形OCED是矩形,利用勾股定理即可求出BC=OE.
解答 证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴∠COD=90°,
∴四边形OCED是矩形,
∴DE=OC,
∵OB=OD,∠BOC=∠ODE=90°,
∴BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{O{D}^{2}+D{E}^{2}}$=OE.
点评 本题考查了菱形的性质,矩形的判定与性质,勾股定理的应用,是基础题,熟记矩形的判定方法与菱形的性质是解题的关键.

练习册系列答案
相关题目
17.形如ax2+bx+c=0的方程是否是一元二次方程的一般形式,下列说法正确的是( )
| A. | a是任意实数 | B. | 与b,c的值有关 | C. | 与a的值有关 | D. | 与a的符号有关 |
18.下列方程中有两个相等实数根的是( )
| A. | 7x2-x-1=0 | B. | 9x2=4(3x-1) | C. | x2+7x+15=0 | D. | 2x2-$\sqrt{3}$x-2=0 |
16.下列事件是随机事件的是( )
| A. | 晴天的早晨,太阳从东方升起 | |
| B. | 测量某天的最低气温,结果为-150℃ | |
| C. | 打开数学课本时刚好翻到第60页 | |
| D. | 在一次体育考试中,小王跑100米用了4秒钟 |
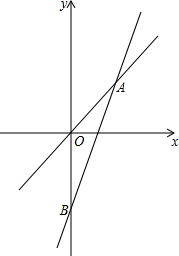 如图,已知一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB
如图,已知一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB 如图,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,若AB=24,则CD的长是12.
如图,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,若AB=24,则CD的长是12.