题目内容
 如图点P在线段AB上,⊙P与x轴相切于D点,且与线段AO相切于C点,已知A、B两点的坐标分别是(8,6),(5,0),
如图点P在线段AB上,⊙P与x轴相切于D点,且与线段AO相切于C点,已知A、B两点的坐标分别是(8,6),(5,0),
求:圆心P的坐标和⊙P的面积.
解:
过A作AE⊥x轴于E,PF∥x轴交OA于F,连接OP、PC、PD,
∵A(8,6),B(5,0),
∴AE=6,OE=8,由勾股定理得:OA=10,
∵⊙P与x轴相切于D点,且与线段AO相切于C点,
∴PC⊥OA,PD⊥OB,
∵PC=PD,
∴∠FOP=∠BOP,
∵PF∥OB,
∴∠FPO=∠BOP,
∴∠FOP=∠FPO,
∴PF=OF,
∵PF∥OB,
∴ =
= ,
,
∴ =
= ,
,
∵ =
= ,
,
∴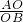 =
= ,
,
即 =
=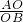 =
=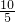 =
= ,
,
∴ =
= ,
,
 =
= ,
,
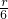 =
= =
= ,
,
r= ×6=2,
×6=2,
而 =
=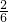 =
= ,
,
BD= BE=
BE= ×(8-5)=1,
×(8-5)=1,
∴OD=5+1=6,
即P的坐标是(6,2),
⊙P的面积是π×22=4π.
分析:过A作AE⊥x轴于E,PF∥x轴交OA于F,连接OP、PC、PD,由勾股定理求出OA=10,求出PC=PD,根据角平分线性质和平行线性质求出∠FOP=∠FPO,推出PF=OF,根据平行线性质得出比例式,求出 =
= ,求出r=2,求出BD、OD,得出P的坐标.
,求出r=2,求出BD、OD,得出P的坐标.
点评:本题考查了切线的性质,角平分线性质,平行线性质,平行线分线段成比例定理,圆的面积,坐标与图形性质等知识点的综合运用,题目综合性比较强,难度偏大.

过A作AE⊥x轴于E,PF∥x轴交OA于F,连接OP、PC、PD,
∵A(8,6),B(5,0),
∴AE=6,OE=8,由勾股定理得:OA=10,
∵⊙P与x轴相切于D点,且与线段AO相切于C点,
∴PC⊥OA,PD⊥OB,
∵PC=PD,
∴∠FOP=∠BOP,
∵PF∥OB,
∴∠FPO=∠BOP,
∴∠FOP=∠FPO,
∴PF=OF,
∵PF∥OB,
∴
 =
= ,
,∴
 =
= ,
,∵
 =
= ,
,∴
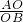 =
= ,
,即
 =
=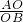 =
=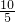 =
= ,
,∴
 =
= ,
, =
= ,
,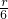 =
= =
= ,
,r=
 ×6=2,
×6=2,而
 =
=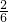 =
= ,
,BD=
 BE=
BE= ×(8-5)=1,
×(8-5)=1,∴OD=5+1=6,
即P的坐标是(6,2),
⊙P的面积是π×22=4π.
分析:过A作AE⊥x轴于E,PF∥x轴交OA于F,连接OP、PC、PD,由勾股定理求出OA=10,求出PC=PD,根据角平分线性质和平行线性质求出∠FOP=∠FPO,推出PF=OF,根据平行线性质得出比例式,求出
 =
= ,求出r=2,求出BD、OD,得出P的坐标.
,求出r=2,求出BD、OD,得出P的坐标.点评:本题考查了切线的性质,角平分线性质,平行线性质,平行线分线段成比例定理,圆的面积,坐标与图形性质等知识点的综合运用,题目综合性比较强,难度偏大.

练习册系列答案
相关题目
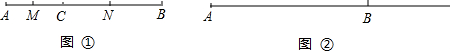
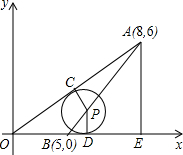 如图点P在线段AB上,⊙P与x轴相切于D点,且与线段AO相切于C点,已知A、B两点的坐标分别是(8,6),(5,0),
如图点P在线段AB上,⊙P与x轴相切于D点,且与线段AO相切于C点,已知A、B两点的坐标分别是(8,6),(5,0), 如图点C在线段AB上,AC=2BC,M、N分别为AC、BC的中点,若BC=4cm,求线段MN的长.
如图点C在线段AB上,AC=2BC,M、N分别为AC、BC的中点,若BC=4cm,求线段MN的长.