题目内容
(1)计算:9
÷3
-
×
;
(2)解方程:2(x+2)2=x2-4;
(3)先化简,再求值:(
-
)•
,其中a=2-
.
| 45 |
|
3
| ||
|
2
|
(2)解方程:2(x+2)2=x2-4;
(3)先化简,再求值:(
| 3a |
| a-1 |
| a |
| a+1 |
| a2-1 |
| a |
| 2 |
考点:二次根式的混合运算,分式的化简求值,解一元二次方程-因式分解法
专题:
分析:(1)先进行二次根式的化简,然后再进行乘法和除法运算;
(2)根据因式分解法解方程;
(3)先进行化简,然后代入数值求解.
(2)根据因式分解法解方程;
(3)先进行化简,然后代入数值求解.
解答:解:(1)原式=27
×
-3
=45
-2
=43
;
(2)原方程可化为:2x2+8x+8=x2-4,
移项得:x2+8x+12=0,
即(x+2)(x+6)=0,
解得:x1=-2,x2=-6;
(3)(
-
)•
=
•
=2a+4,
当a=2-
时,
2a+4=4-2
+4=8-2
.
| 5 |
| ||
| 3 |
|
=45
| 2 |
| 2 |
=43
| 2 |
(2)原方程可化为:2x2+8x+8=x2-4,
移项得:x2+8x+12=0,
即(x+2)(x+6)=0,
解得:x1=-2,x2=-6;
(3)(
| 3a |
| a-1 |
| a |
| a+1 |
| a2-1 |
| a |
=
| 3a2+3a-a2+a |
| a2-1 |
| a2-1 |
| a |
=2a+4,
当a=2-
| 2 |
2a+4=4-2
| 2 |
| 2 |
点评:本题考查了二次根式的混合运算和分式的化简求值等知识,掌握运算法则是解答本题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
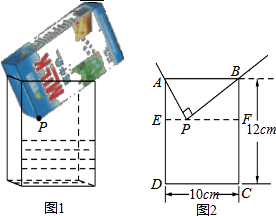 将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=6cm,请根据图中的信息,求出容器中牛奶的高度.
将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=6cm,请根据图中的信息,求出容器中牛奶的高度. 如图,在直角坐标系中,A、B、C、D各点的坐标分别为(-7,7)、(-7,1)、(-3,1)、(-1,4).
如图,在直角坐标系中,A、B、C、D各点的坐标分别为(-7,7)、(-7,1)、(-3,1)、(-1,4).