题目内容
 如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)试探究△DEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△DEF周长的最小值.
考点:菱形的性质,全等三角形的判定与性质
专题:
分析:(1)先判定△ABD与△BCD都是等边三角形,根据等边三角形的性质可得∠BDE=∠C=60°,再求出DE=CF,然后利用“边边角”证明两三角形全等;
(2)根据全等三角形对应边相等可得BE=CF,全等三角形对应角相等可得∠DBE=∠CBF,然后求出∠EBF=60°,再根据等边三角形的判定得解,利用旋转变换解答;
(3)根据EF的最小值为点B到AD的距离
,即EF的最小值是
,即可求出△DEF的周长.
(2)根据全等三角形对应边相等可得BE=CF,全等三角形对应角相等可得∠DBE=∠CBF,然后求出∠EBF=60°,再根据等边三角形的判定得解,利用旋转变换解答;
(3)根据EF的最小值为点B到AD的距离
| 3 |
| 3 |
解答:(1)证明:∵菱形ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2-AE,
又∵DE=AD-AE=2-AE,
∴DE=CF,
在△BDE和△BCF中,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形,
由图可知,△BDE绕点B顺时针旋转60°即可得到△BCF;
(3)解:如图所示:

当BE⊥AD时,△DEF的周长最小,
∵△BDE≌△BCF,
∴DE=FC,
∴DE+DF=AD=2,
故当△DEF的周长最小,则EF最小即可,
∵△BEF是等边三角形,△ABD与△BCD都是等边三角形,
∴BE=ABsin60°=
,
∴△DEF周长的最小值为:2+
.
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2-AE,
又∵DE=AD-AE=2-AE,
∴DE=CF,
在△BDE和△BCF中,
|
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形,
由图可知,△BDE绕点B顺时针旋转60°即可得到△BCF;
(3)解:如图所示:

当BE⊥AD时,△DEF的周长最小,
∵△BDE≌△BCF,
∴DE=FC,
∴DE+DF=AD=2,
故当△DEF的周长最小,则EF最小即可,
∵△BEF是等边三角形,△ABD与△BCD都是等边三角形,
∴BE=ABsin60°=
| 3 |
∴△DEF周长的最小值为:2+
| 3 |
点评:此题主要考查了菱形的性质以及等边三角形的判定与性质和锐角三角函数等知识,根据题意得出EF最小时则△DEF的周长最小得出是解题关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
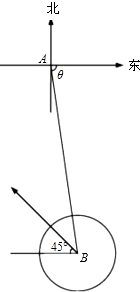 据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ=
据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ=