题目内容
已知x= (n为自然数),问:是否存在自然数n,使代数式19x2+36xy+19y2的值为1 998?若存在,求出n;若不存在,请说明理由.
(n为自然数),问:是否存在自然数n,使代数式19x2+36xy+19y2的值为1 998?若存在,求出n;若不存在,请说明理由.
解:不存在.
∵x+y= 2
2
=n+1-2 +n+n+1+n+2
+n+n+1+n+2 =4n+2.
=4n+2.
xy= •
• =1.
=1.
假设存在n使代数式19x2+36xy+19y2的值为1998.
即19x2+36xy+19y2=1998.
19x2+19y2=1962,(x2+y2)= .
.
(x+y)2= .
.
由已知条件,得x+y=2(2n+1).
∵n为自然数,∴2(2n+1)为偶数,
∴x+y= 不为整数.
不为整数.
∴不存在这样的自然数n.
分析:假设存在,将已知条件化简,求出x+y=2(2n+1),xy=1,代入19x2+36xy+19y2=1998中看是否有符合条件的2n.
点评:此题采用的是反证法:先假设成立,再推翻假设,得出不成立.
∵x+y=
 2
2=n+1-2
 +n+n+1+n+2
+n+n+1+n+2 =4n+2.
=4n+2.xy=
 •
• =1.
=1.假设存在n使代数式19x2+36xy+19y2的值为1998.
即19x2+36xy+19y2=1998.
19x2+19y2=1962,(x2+y2)=
 .
.(x+y)2=
 .
.由已知条件,得x+y=2(2n+1).
∵n为自然数,∴2(2n+1)为偶数,
∴x+y=
 不为整数.
不为整数.∴不存在这样的自然数n.
分析:假设存在,将已知条件化简,求出x+y=2(2n+1),xy=1,代入19x2+36xy+19y2=1998中看是否有符合条件的2n.
点评:此题采用的是反证法:先假设成立,再推翻假设,得出不成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a,b为自然数,且a2-b2=45,则a,b可能的值有( )
| A、1对 | B、2对 | C、3对 | D、4对 |
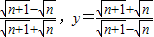 (n为自然数),问:是否存在自然数n,使代数式19x2+36xy+19y2的值为1 998?若存在,求出n;若不存在,请说明理由.
(n为自然数),问:是否存在自然数n,使代数式19x2+36xy+19y2的值为1 998?若存在,求出n;若不存在,请说明理由.