题目内容
已知p,q为自然数,方程2px2-qx+1990=0两根都是质数,则p+q=分析:先设方程的两根是α、β,根据根与系数的关系可得αβ=
=
=
,即αβp=995,而α、β都是质数,故p=1,从而可知方程的两根等于5、199,再利用根与系数的关系,求两根之和α+β=-
=204,
从而可求出q的值,于是可求p+q的值.
| c |
| a |
| 1990 |
| 2p |
| 995 |
| p |
| -q |
| 2 |
从而可求出q的值,于是可求p+q的值.
解答:解:设此方程的两根是α、β,根据题意得
αβ=
=
=
,
即αβp=995,
又∵995=1×5×199,
而5、199都是质数,
∴p=1,
若p=1,则方程的两根就是5、199,
∴α+β=-
=204,
∴q=408,
∴p+q=408+1=409.
故答案是409.
αβ=
| c |
| a |
| 1990 |
| 2p |
| 995 |
| p |
即αβp=995,
又∵995=1×5×199,
而5、199都是质数,
∴p=1,
若p=1,则方程的两根就是5、199,
∴α+β=-
| -q |
| 2 |
∴q=408,
∴p+q=408+1=409.
故答案是409.
点评:此题主要考查了根与系数的关系、质数的定义,注意1不是质数,最小的质数是2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a,b为自然数,且a2-b2=45,则a,b可能的值有( )
| A、1对 | B、2对 | C、3对 | D、4对 |
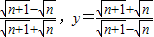 (n为自然数),问:是否存在自然数n,使代数式19x2+36xy+19y2的值为1 998?若存在,求出n;若不存在,请说明理由.
(n为自然数),问:是否存在自然数n,使代数式19x2+36xy+19y2的值为1 998?若存在,求出n;若不存在,请说明理由.