题目内容
8. 如图,在四边形中,∠B=90°,BC=4,AE⊥CD,垂足为E,AE=CE,连接AC,若DE=5,AD=$\sqrt{61}$.求:
如图,在四边形中,∠B=90°,BC=4,AE⊥CD,垂足为E,AE=CE,连接AC,若DE=5,AD=$\sqrt{61}$.求:(1)AC的长;
(2)四边形ABCD的面积.
分析 (1)由垂直的定义得出∠AED=∠AEC=90°,由勾股定理求出AE,得出CE,再由勾股定理求出AC即可;
(2)由勾股定理求出AB,再求出CD,四边形ABCD的面积=△ABC的面积+△ACD的面积,即可得出结果.
解答 解:(1)∵AE⊥CD,
∴∠AED=∠AEC=90°,
∴AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{61-25}$=6,
∴CE=AE=6,
∴AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$;
(2)∵∠B=90°,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{(6\sqrt{2})^{2}-{4}^{2}}$=2$\sqrt{14}$,
∵CD=CE+DE=6+5=11,
∴四边形ABCD的面积=△ABC的面积+△ACD的面积=$\frac{1}{2}$AB×BC+$\frac{1}{2}$CD×AE=$\frac{1}{2}$×2$\sqrt{14}$×4+$\frac{1}{2}$×11×6=4$\sqrt{14}$+33.
点评 本题考查了勾股定理的综合运用以及三角形面积的计算;由勾股定理求出AE、AC、AB是解决问题的关键.

练习册系列答案
相关题目
18.云南某县境内发生地震,某市积极筹集救灾物资260吨从该市区运往该县甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
| 车 型 运往地 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 720 | 800 |
| 小货车 | 500 | 650 |
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
16.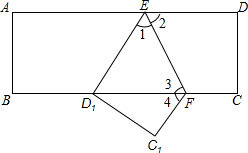 如图,把一个长方形纸片ABCD沿EF折叠后,点D、C分别落在D1、C1位置,其中D1在BC上,则下列结论错误的是( )
如图,把一个长方形纸片ABCD沿EF折叠后,点D、C分别落在D1、C1位置,其中D1在BC上,则下列结论错误的是( )
 如图,把一个长方形纸片ABCD沿EF折叠后,点D、C分别落在D1、C1位置,其中D1在BC上,则下列结论错误的是( )
如图,把一个长方形纸片ABCD沿EF折叠后,点D、C分别落在D1、C1位置,其中D1在BC上,则下列结论错误的是( )| A. | ∠C1=∠C1D1E=90° | B. | ∠1+∠2+∠4=180° | C. | CF=C1F=CD | D. | ∠BD1E=2∠3 |
3.2015年十一国庆长假提前到9月29日,黄金周期间外出旅游更为火爆,若旅游区的门票为60元/张,某旅游区的开放时间为每天10小时,并每小时对进入旅游区的游客人数进行一次统计,下表是9月30日对进入旅游区人数的7次抽样统计数据:
那么从9月29日至10月5日旅游区门票收入是多少?( )
| 记数的次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 |
| 每小时进入旅游区的人数 | 318 | 310 | 310 | 286 | 280 | 312 | 284 |
| A. | 900000元 | B. | 1260000元 | C. | 191600元 | D. | 162000元 |



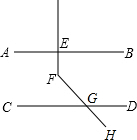 如图,AB∥CD,EF⊥AB,FH交CD于G,若∠EFH=125°,则∠DGH=35°.
如图,AB∥CD,EF⊥AB,FH交CD于G,若∠EFH=125°,则∠DGH=35°.