题目内容
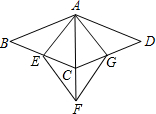如图，四边形ABCD与四边形AEFG都是菱形，其中点C在AF上，点E，G分别在BC，CD上，若∠BAD=135°，∠EAG=75°，AE=2，则AB=考点：菱形的性质
专题：
分析：利用菱形的性质，对角线平分每组对角得出∠BAE的度数，进而得出∠B的度数，即可得出BM，AM的长，进而得出答案即可．
解答：
解：过点E作EM⊥AB于点M，
∵四边形ABCD与四边形AEFG都是菱形，∠BAD=135°，∠EAG=75°，
∴∠BAE=∠DAG=
（∠BAD-∠EAG）=30°，∠B=45°，
∵AE=2，
∴ME=1，AM=
，
∴BM=ME=1，
∴AB=1+
．
故答案为：1+
．
解：过点E作EM⊥AB于点M，∵四边形ABCD与四边形AEFG都是菱形，∠BAD=135°，∠EAG=75°，
∴∠BAE=∠DAG=
| 1 |
| 2 |
∵AE=2，
∴ME=1，AM=
| 3 |
∴BM=ME=1，
∴AB=1+
| 3 |
故答案为：1+
| 3 |
点评：此题主要考查了菱形的性质以及勾股定理等知识，得出∠BAE的度数是解题关键．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）| A、∠B=∠D=90° |
| B、∠BCA=∠DCA |
| C、∠BAC=∠DAC |
| D、CB=CD |
下列条件不可以判定两个直角三角形全等的是（ ）
| A、两条直角边对应相等 |
| B、斜边和一直角边对应相等 |
| C、斜边和一锐角对应相等 |
| D、两个角对应相等 |
对下列各式计算结果的符号判断正确的一个是（ ）
A、（-2）×（-2
| ||||
| B、（-5）-5+1＞0 | ||||
C、（-1）+（-
| ||||
| D、（-1）×（-2）＜0 |
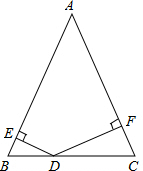如图，在△ABC中，AB=AC，D是线段BC上任意一点，过D分别向AB、AC引垂线，垂足分别为E、F点．3的相反数的倒数是（ ）
| A、3 | ||
B、-
| ||
C、
| ||
| D、-3 |