Question

13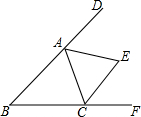．如图，已知∠B=46°，△ABC的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=67°．

Answer 1

分析 根据三角形内角和定理、角平分线的定义以及三角形外角定理求得$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=$\frac{1}{2}$（∠B+∠B+∠1+∠2）=113°；最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数．

解答 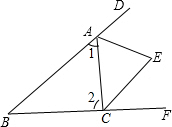解：∵三角形的外角∠DAC和∠ACF的平分线交于点E，
∴∠EAC=$\frac{1}{2}$∠DAC，∠ECA=$\frac{1}{2}$∠ACF，
∵∠DAC=∠B+∠2，∠ACF=∠B+∠1
∴$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=$\frac{1}{2}$（∠B+∠2）+$\frac{1}{2}$（∠B+∠1）=$\frac{1}{2}$（∠B+∠B+∠1+∠2），
∵∠B=46°（已知），∠B+∠1+∠2=180°（三角形内角和定理），
∴$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=113°
∴∠AEC=180°-（$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF）=67°．
故答案是：67°．

点评 本题考查了三角形内角和定理、三角形外角性质．解题时注意挖掘出隐含在题干中已知条件“三角形内角和是180°”．