题目内容
15.一个口袋中6个黑球,10个白球,这些球除了颜色外完全相同.充分搅匀后随机摸出一球,发现是黑球.(1)如果将这个黑球放回,再摸出一球,那么它是白球的概率是多少?
(2)如果这个黑球不放回,再摸出一球,那么它是白球的概率是多少?
分析 (1)摸出一个黑球放回对第二次摸到白球没有影响,直接利用概率公式求解即可;
(2)如果这个黑球不放回,则总数减少1,再利用概率公式求解即可.
解答 解:(1)如果将白球放回,再摸出一球P(摸到的球是白球)=$\frac{10}{10+6}$=$\frac{5}{8}$;
(2)如果这个黑球不放回,再摸出一球,有10个白球和5个黑球,再摸出一球P(摸到的球是白球)=$\frac{10}{10+5}$=$\frac{2}{3}$.
点评 本题考查了概率的公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
6.质检员抽查某零件的质量,超过规定尺寸的记为正数,不足规定尺寸的记为负数,结果第一个0.13mm,第二个-0.12mm,第三个0.15mm,第四个0.11mm,则质量最好的零件是( )
| A. | 第一个 | B. | 第二个 | C. | 第三个 | D. | 第四个 |
5.-9的倒数是( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | $-\frac{1}{9}$ |
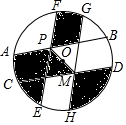 如图,一个半径为2cm的圆盘被分割成十个区域.其中,弦AB、CD关于圆心O对称,EF、GH关于圆心O对称,向盘中投掷一物体,则物体落在阴影部分的概率为$\frac{1}{2}$.
如图,一个半径为2cm的圆盘被分割成十个区域.其中,弦AB、CD关于圆心O对称,EF、GH关于圆心O对称,向盘中投掷一物体,则物体落在阴影部分的概率为$\frac{1}{2}$.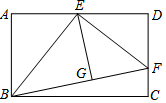 如图,已知矩形ABCD中,点E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=6,BC=4$\sqrt{6}$,则下列说法中正确的个数有( )
如图,已知矩形ABCD中,点E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=6,BC=4$\sqrt{6}$,则下列说法中正确的个数有( ) 如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是-1≤x≤2.
如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是-1≤x≤2.