题目内容
8．
如图，某宾馆在重新装修后，准备在大厅的主楼梯上铺上红色地毯，已知这种地毯每平方米售价20元，主楼梯宽2米．则购地毯至少需要280元．
分析 根据题意，结合图形，先把楼梯的横竖向上向左平移，构成一个矩形，再求得其面积，则购买地毯的钱数可求．
解答 解：利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，
∵所有竖直台阶的长为5，水平台阶的长为$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴地毯的长度为3+4=7米，地毯的面积为7×2=14平方米，
∴购买这种地毯至少需要20×14=280元．
故答案为：280．
点评 本题考查了勾股定理的运用，解决此题的关键是要注意利用平移的知识，把要求的所有线段平移到一条直线上进行计算．
练习册系列答案
阅读快车系列答案
相关题目
16．若α为锐角，且sinα=$\frac{4}{5}$，则tanα为（ ）
| A． | $\frac{9}{25}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
20．
如图所示，C是线段AB的中点，D是线段BC的中点，下列等式不正确的是（ ）
如图所示，C是线段AB的中点，D是线段BC的中点，下列等式不正确的是（ ）| A． | CD=BC-DB | B． | CD=AD-AC | C． | $CD=\frac{1}{2}AB-BD$ | D． | $CD=\frac{1}{3}AB$ |
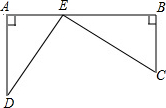如图，铁路上A、B两站相距25km，C，D为两村庄，且DA⊥AB，CB⊥AB，已知AD=15km，CB=10km，在AB上是否存在一点E，使它到C、D两村庄的距离相等？若存在，求出此时AE的距离；若不存在，请说明理由．
18．
如图，直线a∥b，直线a、b被直线c所截，∠1=40°，则∠2的度数为（ ）
如图，直线a∥b，直线a、b被直线c所截，∠1=40°，则∠2的度数为（ ）| A． | 40° | B． | 80° | C． | 140° | D． | 160° |