题目内容
16.已知:在四边形ABCD中,∠BAC+∠BDC=180°,∠ABC=∠BAC=60°,如图1,连结BC、AD.(1)求证:∠ADB=∠ADC.
(2)如图2,过B作BH⊥AD于H,延长BH交AC于E,连结CH并延长交B于F,若AE=BF,BD=4,求AD的长.
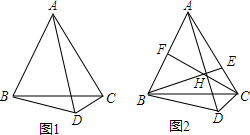
分析 (1)首先利用∠ACB+∠ADB=180°,得出A、B、C、D四点共圆,进而得出弦AC、BC所对的圆周角相等,即∠ADC=∠BDC得出答案即可;
(2)根据∠ADB=∠ADC,于是得到∠BDC=180°-∠BAC=120°,求得∠BDH=60°,根据已知条件得到∠DBH=30°,由直角三角形的性质得到DH=$\frac{1}{2}$BD=2,推出△FBC≌△ABE,根据全等三角形的性质得到∠BCF=∠ABE.由于∠BHF=∠BCF+∠CBH=∠ABE+∠CBH=60°,于是得到∠CHD=30°=∠DBH推出∠DCH=90°,根据直角三角形的性质得到CD=$\frac{1}{2}$DH=1,延长CD到G,使DG=DB=4,连接BG.于是得到△BDG为等边三角形,根据等边三角形的性质得到BG=BD,根据等腰三角形的性质得到∠GBD=∠CBA=60°,证得△GBC≌△DBA,根据全等三角形的性质即可得到结论.
解答 (1)证明:∵∠ABC=∠BAC=60°,
∴AC=BC,
∵∠ACB+∠ADB=180°,
∴A、B、C、D四点共圆,
∵AC=BC,
∴弦AC、BC所对的圆周角相等,
∴∠ADC=∠ADB;
(2)解:∵∠ADC=∠ADB;
∴∠BDC=180°-∠BAC=120°,
∴∠BDH=60°,
∵BH⊥AD,
∴∠DBH=30°,DH=$\frac{1}{2}$BD=2,
在△FBC与△ABE中,
$\left\{\begin{array}{l}{BC=AB}\\{∠FBC=∠BAE}\\{BF=AE}\end{array}\right.$,
∴△FBC≌△ABE,
∴∠BCF=∠ABE,
∵∠BHF=∠BCF+∠CBH=∠ABE+∠CBH=60°,
∴∠CHD=30°=∠DBH,
∵∠CDH=∠BDH=60°,
∴∠DCH=90°,CD=$\frac{1}{2}$DH=1,
延长CD到G,使DG=DB=4,连接BG.
则△BDG为等边三角形,∴BG=BD;∠GBD=∠CBA=60°,
∴∠GBC=∠DBA,
在△GBC与△DBA中,
$\left\{\begin{array}{l}{∠GBC=∠DBA}\\{∠G=∠ADB}\\{BC=AB}\end{array}\right.$,
∴△GBC≌△DBA,
∴AD=CG=BD+DC=4+1=5.
点评 此题主要考查了四点共圆以及圆周角定理,利用已知得出弦AC、BC所对的圆周角相等是解题关键

| A. | -6℃ | B. | -2℃ | C. | 8℃ | D. | -8℃ |
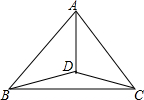 如图,AB=AC,∠CBD=∠BCD,∠BDC=150°,求∠BDA的度数.
如图,AB=AC,∠CBD=∠BCD,∠BDC=150°,求∠BDA的度数.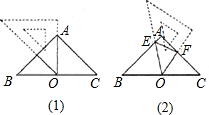 在△ABC中,AB=AC=2,∠BAC=90°,取一块含45°角的直角三角形纸板,将45°角的顶点放在斜边BC的中点O处(如图①),顺时针方向旋转三角尺,使45°角的两边与AB、AC分别交于点E、F(如图②).设BE=x,CF=y,求y与x的函数表达式,并写出x的取值范围.
在△ABC中,AB=AC=2,∠BAC=90°,取一块含45°角的直角三角形纸板,将45°角的顶点放在斜边BC的中点O处(如图①),顺时针方向旋转三角尺,使45°角的两边与AB、AC分别交于点E、F(如图②).设BE=x,CF=y,求y与x的函数表达式,并写出x的取值范围.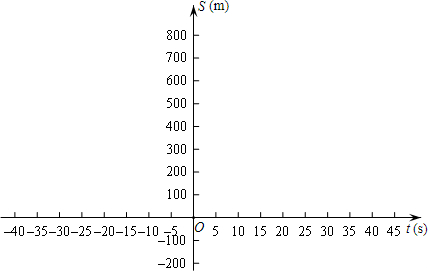
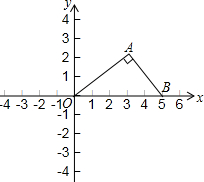 如图所示,在平面直角坐标系内有A、B两点,△A0B中∠OAB=90°,AO=4,AB=3,BO=5,点A横坐标与点B横坐标的比为16:25.
如图所示,在平面直角坐标系内有A、B两点,△A0B中∠OAB=90°,AO=4,AB=3,BO=5,点A横坐标与点B横坐标的比为16:25.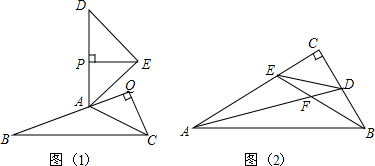
 中
中 的取值范围是_____.
的取值范围是_____.