Question

1．飞机着陆后滑行的距离S（单位：m）关于滑行时间t（单位：s）的函数解析式是：S=60t-1.5t²
（1）直接指出飞机着陆时的速度；
（2）直接指出t的取值范围；
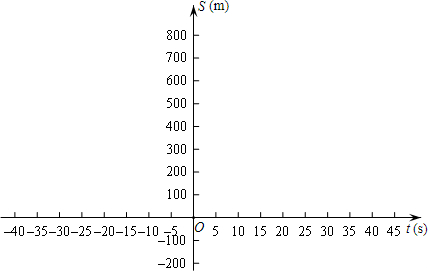
（3）画出函数S的图象并指出飞机着陆后滑行多远才能停下来？

Answer 1

分析 （1）直接由函数解析式得出答案即可；
（2）由于飞机着陆，不会倒着跑，所以当S取得最大值时，t也取得最大值，求得t的取值范围即可；
（3）利用配方法求得函数的最值，也就是飞机着陆后滑行的最远距离．

解答 解：（1）飞机着陆时的速度V=60；
（2）当S取得最大值时，飞机停下来，
则S=60t-1.5t²=-1.5（x-20）²+600，
此时t=20
因此t的取值范围是0≤t≤20；
（3）如图，
S=60t-1.5t²=-1.5（x-20）²+600．
飞机着陆后滑行600米才能停下来．

点评 此题考查二次函数的实际运用，运用二次函数求最值问题常用公式法或配方法是解题关键．