题目内容
5.(1)如图(1),在△BAC和△DAE中,BA=AD,CA=EA,∠BAC+∠DAE=180°,求证:△BAC和△DAE的面积相等.(2)如图(2),在Rt△ABC中,∠ACB=90°,AD,BE分别平分∠CAB,∠CBA,且AD,BE交于点F,求证:四边形ABDE的面积是△AFB面积的2倍.
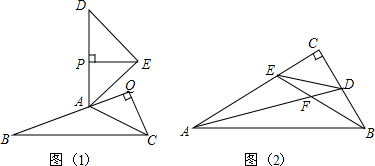
分析 (1)根据已知条件得到∠PAE=∠QAC,推出△APE≌△AQC,根据全等三角形的性质得到PE=CQ,即可得到结论;
(2)在AB上截取AI=AE,BG=BD,连接IF、FG,过点E作EM⊥AD于点M,过点G作GN⊥IF于点N,易证△AFE≌△AFI,△BFD≌△BFG,根据三角形的内心的性质可求得∠AFB=90°+$\frac{1}{2}$∠ABC=135°,然后求出∠AFE、∠AFI、∠IFG的度数,然后根据正弦定理求出△EFD和△IFG的面积,最后即可求出四边形ABDE的面积.
解答 证明:(1)∵∠BAC+∠DAE=180°,∠BAC+∠QAC=180°,
∴∠PAE=∠QAC,
在△APE与△AQC中,
$\left\{\begin{array}{l}{∠APE=∠Q}\\{∠PAE=∠QAC}\\{AE=AC}\end{array}\right.$,
∴△APE≌△AQC,
∴PE=CQ,
∵BA=AD,
∴S△ABC=$\frac{1}{2}•AB•CQ$,S△ADE=$\frac{1}{2}•$AD•PE,
∴△BAC和△DAE的面积相等;
(2)解:如图(2)在AB上截取AI=AE,BG=BD,连接IF、FG,过点E作EM⊥AD于点M,过点G作GN⊥IF于点N,
在△AFE和△AIF中,
$\left\{\begin{array}{l}{AE=AF}\\{∠EAF=∠IAF}\\{AF=AF}\end{array}\right.$,
∴△AFE≌△AIF(SAS),
同理可得:△BFD≌△BFG,
∵点F是角平分线AD、BE的交点,
∴点F是△ABC的内心,
∴∠AFB=90°+$\frac{1}{2}$∠ABC=135°,
∴∠AFE=∠BFD=180°-∠AFB=45°,
∴∠AFI=∠AFE=∠BFD=∠BFG=45°,
∴∠IFG=135°-45°-45°=45°,
∴S△EFD=$\frac{1}{2}$FD•EM=$\frac{1}{2}$EF•FDsin45°,
S△IFG=$\frac{1}{2}$FF•GN=$\frac{1}{2}$IF•FGsin45°,
∴S△EFD=S△IFG,
∴S四边形ABDE=S△EFD+S△AFE+S△AFB+S△BFD
=S△IFG+S△AIF+S△FIG+S△AFB
=2S△AFB.
点评 本题考查了全等三角形的判定和性质,面积及等积变换,解答本题的关键是作出合适的辅助线,利用三角形的等积变换求出四边形ABDE的面积,难度较大.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案

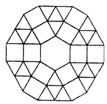 某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.)
某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.)  (m≠0)的图像交于点A(-1,6)、B(a,-2).
(m≠0)的图像交于点A(-1,6)、B(a,-2).
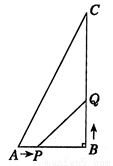
 时,求△PBQ的面积;
时,求△PBQ的面积; 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?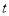 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似.