题目内容
7.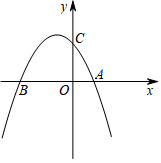 如图,抛物线y=ax2-x+4与x轴交于点A、B,B点的坐标为(-4,0),与y轴交于点C.
如图,抛物线y=ax2-x+4与x轴交于点A、B,B点的坐标为(-4,0),与y轴交于点C.(1)求抛物线的解析式和对称轴.
(2)连接AC、BC,在x轴下方的抛物线上求一点M,使△ABM与△ABC的面积相等.
(3)在x轴下方作平行于x轴的直线l,与抛物线交于点D、E两点(点D在对称轴的左侧).过点D、E分别作x轴的垂线,垂足分别为G、F,当矩形DEFG中DE=2DG时,求D点的坐标.
分析 (1)把B点坐标代入y=ax2-x+4中求出a的值即可得到抛物线解析式;
(2)先利用y轴上点的坐标特征写出C(0,4),再利用三角形面积公式得到点M、C点到x轴的距离相等,即点M的纵坐标为-4,然后解方程-$\frac{1}{2}$x2-x+4=-4即可得到M点的坐标;
(3)如图,设D(t,-$\frac{1}{2}$t2-t+4)(t<-1),利用DE=2DG和抛物线的对称性得到1-t=-(-$\frac{1}{2}$t2-t+4),然后解方程求出t即可得到D点坐标.
解答 解:(1)把B(-4,0)代入y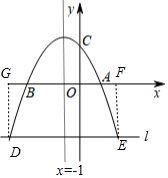 =ax2-x+4得16a+4+4=0,解得a=-$\frac{1}{2}$,
=ax2-x+4得16a+4+4=0,解得a=-$\frac{1}{2}$,
所以抛物线的解析式为y=-$\frac{1}{2}$x2-x+4,
抛物线的对称轴为直线x=-$\frac{-1}{2×(-\frac{1}{2})}$=-1;
(2)当x=0时,y=-$\frac{1}{2}$x2-x+4=4,则C(0,4),
∵△ABM与△ABC的面积相等,
∴点M的纵坐标为-4,
当y=-4时,-$\frac{1}{2}$x2-x+4=-4,解得x1=-1+$\sqrt{17}$,x2=-1-$\sqrt{17}$,
∴M点的坐标为(-1+$\sqrt{17}$,-4)或(-1-$\sqrt{17}$,-4);
(3)如图,设D(t,-$\frac{1}{2}$t2-t+4)(t<-1)
∵DE=2DG,
∴-1-t=-(-$\frac{1}{2}$t2-t+4),
整理得t2+4t-6=0,解得t1=-2-$\sqrt{10}$,t2=-2+$\sqrt{10}$,
∴D(-2-$\sqrt{10}$,-1-$\sqrt{10}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会解一元二次方程;理解坐标与图形性质.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | a3•a4=a12 | B. | m3+m4=m7 | C. | (a+b)2=a2+b2 | D. | n6÷n3=n3 |
| A. | x3+2x=3x4 | B. | x8+x2=x10 | C. | (-x)4•x2=x6 | D. | (-x5)2=-x10 |
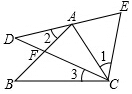 如图所示,点A在DE上,点F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )
如图所示,点A在DE上,点F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )| A. | AC | B. | BC | C. | AB+AC | D. | AB |
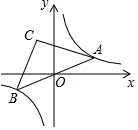 如图,点A是双曲线y=$\frac{6}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{6}{x}$.
如图,点A是双曲线y=$\frac{6}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{6}{x}$. 如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F. 如图,在四边形ABCD中,AB=CD,AD=BC,点O为BD上任意一点,过点O的直线分别交AD,BC于M,N两点.求证:∠1=∠2.
如图,在四边形ABCD中,AB=CD,AD=BC,点O为BD上任意一点,过点O的直线分别交AD,BC于M,N两点.求证:∠1=∠2.