题目内容
9.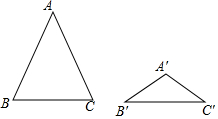 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠A与∠A′互补,则△ABC与△A′B′C′的面积比为( )
如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠A与∠A′互补,则△ABC与△A′B′C′的面积比为( )| A. | $\sqrt{5}$:$\sqrt{3}$ | B. | 5:3 | C. | 25:9 | D. | 5$\sqrt{5}$:3$\sqrt{3}$ |
分析 先根据等腰三角形的性质得到∠B=∠C,∠B′=∠C′,根据三角函数的定义得到AD=AB•sinB,A′D′=A′B′•sinB′,BC=2BD=2AB•cosB,B′C′=2B′D′=2A′B′•cosB′,然后根据三角形面积公式即可得到结论.
解答 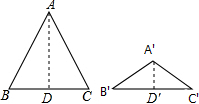 解:过A 作AD⊥BC于D,过A′作A′D′⊥B′C′于D′,
解:过A 作AD⊥BC于D,过A′作A′D′⊥B′C′于D′,
∵△ABC与△A′B′C′都是等腰三角形,
∴∠B=∠C,∠B′=∠C′,BC=2BD,B′C′=2B′D′,
∴AD=AB•cosBAD,A′D′=A′B′•cosB′A′D′,BC=2BD=2AB•sinBAD,B′C′=2B′D′=2A′B′•sinB′A′D′,
∵∠A与∠A′互补,
∴sinB=cosB′,sinB′=cosB,
∵S△BAC=$\frac{1}{2}$AD•BC=$\frac{1}{2}$AB•sinB•2AB•cosB=25sinB•cosB,
S△A′B′C′=$\frac{1}{2}$A′D′•B′C′=$\frac{1}{2}$A′B′•cosB′•2A′B′•sinB′=9sinB′•cosB′,
∴S△BAC:S△A′B′C′=25:9.
故选C.
点评 本题考查了互余两角的关系,解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了等腰三角形的性质和三角形面积公式.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.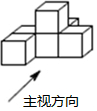 由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )
由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )
 由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )
由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )| A. | 左视图与主视图相同 | B. | 俯视图与主视图相同 | ||
| C. | 左视图与俯视图相同 | D. | 三个视图都相同 |
4.已知关于x的一元一次方程(a+3)x|a|-2+6=0,则a的值为( )
| A. | 3 | B. | -3 | C. | ±3 | D. | ±2 |