题目内容
已知关于x的一元二次方程(m-1)x2+(2m-3)x-m=0的一个根大于
,另一根小于-1,求实数m的取值范围.
| 1 |
| 2 |
考点:一元二次方程根的分布
专题:
分析:此题需要分类讨论:m-1>0和m-1<0两种情况.设f(x)=(m-1)x2+(2m-3)x-m,则
或
.通过解不等式组来求m的取值范围.
|
|
解答:解:设f(x)=(m-1)x2+(2m-3)x-m.
①当m-1>0时,
,即
,
解得 1<m<7;
②当m-1<0时,
,即
,
该方程组无解.
综上所述,m的取值范围是1<m<7.
①当m-1>0时,
|
|
解得 1<m<7;
②当m-1<0时,
|
|
该方程组无解.
综上所述,m的取值范围是1<m<7.
点评:本题主要考查一元二次方程的根的分布,即考查实根分布问题,解决此类问题的关键是熟练掌握一元二次函数的图象.

练习册系列答案
相关题目
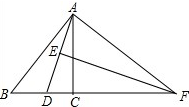 如图,已知△ABC中,AD平分∠BAC,EF是AD的垂直平分线,交BC延长线于F,求证:DF2=BF•CF.
如图,已知△ABC中,AD平分∠BAC,EF是AD的垂直平分线,交BC延长线于F,求证:DF2=BF•CF.
 如图是窗子的形状,它是由上下连成一体的两个矩形构成,已知窗框的用料是6m,要使窗子能透过最多的光线,问窗子的各边长是多少?
如图是窗子的形状,它是由上下连成一体的两个矩形构成,已知窗框的用料是6m,要使窗子能透过最多的光线,问窗子的各边长是多少?