题目内容
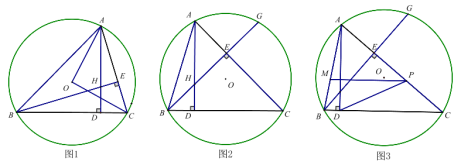
【题目】如图,在![]() 中,半径
中,半径![]() 直径
直径![]() 与
与![]() 相切于点
相切于点![]() 连接
连接![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
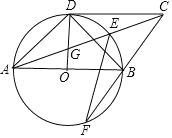
![]() 求证:
求证: ![]() ;
;
![]() 若
若![]()
①求证:四边形![]() 是平行四边形;
是平行四边形;
②连接![]() ,当
,当![]() 的半径为
的半径为![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)详见解析;(2)①详见解析;②![]()
【解析】
(1)先利用切线的性质得到OD⊥CD,再证明AB∥CD,然后利用平行线的性质和圆周角定理得到结论;
(2)①设⊙O的半径为r,利用正切的定义得到OG=![]() r,则DG=
r,则DG=![]() r,则CD=3DG=2r,然后根据平行线的判定得到结论;
r,则CD=3DG=2r,然后根据平行线的判定得到结论;
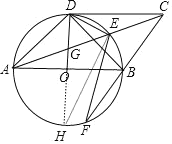
②作直径DH,连接HE,如图,先计算出AG=![]() ,CG=2
,CG=2![]() ,再证明△CDE∽△CAD,然后利用相似比计算DE的长.
,再证明△CDE∽△CAD,然后利用相似比计算DE的长.
![]() 证明:
证明: ![]() 与
与![]() 相切于点
相切于点![]() ,
,
![]() ,
,
![]() 半径
半径![]() 直径
直径![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 证明:
证明:![]() ,
,
![]()
设![]() 的半径为
的半径为![]() ,
,
在![]() 中,
中, ![]()
![]()
![]()
在![]() 中,
中,![]()
![]() ,
,
![]() ,
,
而![]() ,
,
![]() 四边形
四边形![]() 是平行四边形:
是平行四边形:
![]() 作直径
作直径![]() 连接
连接![]() ,如图,
,如图,
∵![]() ,半径为3
,半径为3
∴![]()
∵四边形![]() 是平行四边形,OD⊥CD,
是平行四边形,OD⊥CD,
∴![]() ,
,
![]() 为直径,
为直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
而![]()
![]() ,
,
![]() ,即
,即![]()
![]() .
.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目