Ő‚ńŅńŕ»›
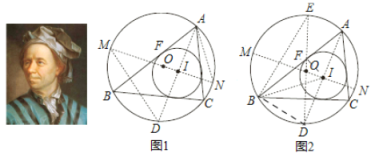
°ĺŐ‚ńŅ°Ņ»ÁÕľňý ĺ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶxOy÷–£¨Rt°ųAOBĶń÷ĪĹ«ĪŖOB£¨OA∑÷Īū‘ŕx÷Š…ŌļÕy÷Š…Ō£¨∆š÷–OA=2£¨OB=4£¨Ō÷ĹęRt°ųAOB»∆◊Ň÷ĪĹ«∂•Ķ„Oįīńś Ī’Ž∑ĹŌÚ–ż◊™90°„Ķ√ĶĹ°ųCOD£¨“—÷™“ĽŇ◊őÔŌŖĺ≠ĻżC°ĘD°ĘB»żĶ„£ģ
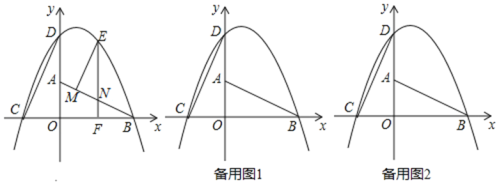
£®1£©ł√Ň◊őÔŌŖĶńĹ‚őŲ Ĺő™°°°°£Ľ
£®2£©…ŤĶ„E «Ň◊őÔŌŖ…ŌőĽ”ŕĶŕ“ĽŌůŌřĶń∂ĮĶ„£¨ĻżĶ„E◊ųEF°Õx÷Š”ŕĶ„F£¨≤ĘĹĽ÷ĪŌŖAB”ŕN£¨ĻżĶ„E‘Ŕ◊ųEM°ÕAB”ŕĶ„M£¨«ů°ųEMN÷‹≥§Ķń◊Óīů÷Ķ£Ľ
£®3£©ĶĪ°ųEMNĶń÷‹≥§◊Óīů Ī£¨‘ŕ÷ĪŌŖEF…Ō «∑Ůīś‘ŕĶ„Q£¨ ĻĶ√°ųQCD «“‘CDő™÷ĪĹ«ĪŖĶń÷ĪĹ«»żĹ«–ő£Ņ»Űīś‘ŕ«Ž«ů≥ŲĶ„QĶń◊ÝĪÍ£¨»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©y=©Ā![]() +x+4£Ľ£®2£©◊Óīů÷Ķő™
+x+4£Ľ£®2£©◊Óīů÷Ķő™![]() £Ľ£®3£©īś‘ŕ£¨ĶĪĶ„QĶń◊ÝĪÍő™£®
£Ľ£®3£©īś‘ŕ£¨ĶĪĶ„QĶń◊ÝĪÍő™£®![]() £¨
£¨![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨
£¨![]() £© Ī£¨ ĻĶ√°ųQCD «“‘CDő™÷ĪĹ«ĪŖĶń÷ĪĹ«»żĹ«–ő
£© Ī£¨ ĻĶ√°ųQCD «“‘CDő™÷ĪĹ«ĪŖĶń÷ĪĹ«»żĹ«–ő
°ĺĹ‚őŲ°Ņ
£®1£©…ŤŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™![]() £ģ”…ŌŖ∂őOA°ĘOBĶń≥§∂»Ņ…Ķ√≥ŲĶ„A°ĘBĶń◊ÝĪÍ£¨‘Ŕ”…–ż◊™ĶńŐō–‘Ņ…Ķ√≥ŲĶ„C°ĘDĶń◊ÝĪÍ£¨”…Ķ„B°ĘC°ĘD»żĶ„Ķń◊ÝĪÍņŻ”√īż∂®ŌĶ ż∑®ľīŅ…«ů≥ŲŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£ģ”…ŌŖ∂őOA°ĘOBĶń≥§∂»Ņ…Ķ√≥ŲĶ„A°ĘBĶń◊ÝĪÍ£¨‘Ŕ”…–ż◊™ĶńŐō–‘Ņ…Ķ√≥ŲĶ„C°ĘDĶń◊ÝĪÍ£¨”…Ķ„B°ĘC°ĘD»żĶ„Ķń◊ÝĪÍņŻ”√īż∂®ŌĶ ż∑®ľīŅ…«ů≥ŲŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©‘ŕRt°ųAOB÷–£¨«ů≥Ų°ŌABOĶń’żŌ“”ŗŌ“÷Ķ£¨‘Ŕłýĺ›Ōŗň∆»żĹ«–őĶńŇ–∂®∂®ņŪ’“≥Ų°ųEMN°◊°ųBFN£¨ī”∂ÝĶ√≥Ų°ŌMEN=°ŌFBN£¨”√ENĶń≥§∂»ņīĪŪ ĺ≥ŲEMļÕMNĶń≥§∂»£¨”…Ķ„A°ĘBĶń◊ÝĪÍņŻ”√īż∂®ŌĶ ż∑®«ů≥Ų÷ĪŌŖABĶńļĮ żĹ‚őŲ Ĺ£¨…Ť≥ŲĶ„EĶń◊ÝĪÍő™![]() £®0£ľt£ľ4£©£¨ľīŅ…’“≥ŲĶ„NĶń◊ÝĪÍő™
£®0£ľt£ľ4£©£¨ľīŅ…’“≥ŲĶ„NĶń◊ÝĪÍő™![]() £¨ī”∂ÝĶ√≥ŲŌŖ∂őENĶń≥§∂»£¨ĹęEN°ĘMN°ĘEMŌŗľ”ľīŅ…Ķ√≥Ų°ųEMNĶń÷‹≥§£¨łýĺ›∂ĢīőļĮ żĶń–‘÷ Ņ…«ů≥ŲENĶń◊Óīů÷Ķ£¨”…īňľīŅ…Ķ√≥ŲĹŠ¬Ř£Ľ
£¨ī”∂ÝĶ√≥ŲŌŖ∂őENĶń≥§∂»£¨ĹęEN°ĘMN°ĘEMŌŗľ”ľīŅ…Ķ√≥Ų°ųEMNĶń÷‹≥§£¨łýĺ›∂ĢīőļĮ żĶń–‘÷ Ņ…«ů≥ŲENĶń◊Óīů÷Ķ£¨”…īňľīŅ…Ķ√≥ŲĹŠ¬Ř£Ľ
£®3£©ĹŠļŌ£®2£©ĶńĹŠ¬ŘŅ…÷™÷ĪŌŖEFĶńĹ‚őŲ Ĺő™![]() £¨∑÷°ŌQDC=90°„ļÕ°ŌDCQ=90°„ŃĹ÷÷«ťŅŲņīŅľ¬«£¨ņŻ”√Ōŗň∆»żĹ«–őĶń–‘÷ ’“≥ŲŌŗň∆ĪŖĶńĪ»ņżĻōŌĶņī’“≥ŲŌŖ∂őĶń≥§∂»£¨‘Ŕłýĺ›Ķ„”ŽĶ„ľšĶń żŃŅĻōŌĶľīŅ…’“≥ŲĶ„QĶń◊ÝĪÍ£ģ
£¨∑÷°ŌQDC=90°„ļÕ°ŌDCQ=90°„ŃĹ÷÷«ťŅŲņīŅľ¬«£¨ņŻ”√Ōŗň∆»żĹ«–őĶń–‘÷ ’“≥ŲŌŗň∆ĪŖĶńĪ»ņżĻōŌĶņī’“≥ŲŌŖ∂őĶń≥§∂»£¨‘Ŕłýĺ›Ķ„”ŽĶ„ľšĶń żŃŅĻōŌĶľīŅ…’“≥ŲĶ„QĶń◊ÝĪÍ£ģ
Ĺ‚£ļ£®1£©…ŤŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™![]() £ģ
£ģ
°ŖOA=2£¨OB=4£¨
°ŗĶ„A£®0£¨2£©£¨Ķ„B£®4£¨0£©£¨
”…–ż◊™ĶńŐō–‘Ņ…÷™£ļ
Ķ„C£®©Ā2£¨0£©£¨Ķ„D£®0£¨4£©£ģ
ĹęĶ„B£®4£¨0£©°ĘĶ„C£®©Ā2£¨0£©°ĘĶ„D£®0£¨4£©īķ»ŽĶĹŇ◊őÔŌŖĹ‚őŲ ĹĶ√£ļ
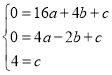 £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ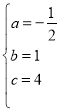 £ģ
£ģ
°ŗł√Ň◊őÔŌŖĶńĹ‚őŲ Ĺő™![]() £ģ
£ģ
Ļ īūįłő™£ļ![]() £ģ
£ģ
£®2£©“ņ’’Ő‚“‚Ľ≠≥ŲÕľ–ő£¨»ÁÕľ1ňý ĺ£ģ
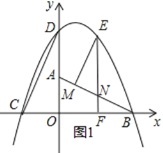
‘ŕRt°ųAOB÷–£¨OA=2£¨OB=4£¨
°ŗAB=![]()
![]() £¨
£¨
°ŗsin°ŌABO=![]() £¨cos°ŌABO=
£¨cos°ŌABO=![]() £ģ
£ģ
°ŖEM°ÕAB£¨EF°ÕOB£¨
°ŗ°ŌEMN=°ŌBFN=90°„£ģ
°Ŗ°ŌBNF=°ŌENM£¨
°ŗ°ųEMN°◊°ųBFN£¨
°ŗ°ŌMEN=°ŌFBN£ģ
‘ŕRt°ųEMN÷–£¨sin°ŌMEN=![]() £¨cos°ŌMEN=
£¨cos°ŌMEN=![]() £¨
£¨
°ŗMN=ENsin°ŌMEN=ENsin°ŌABO=![]() EN£¨
EN£¨
EM=ENcos°ŌMEN=ENcos°ŌABO=![]() EN£ģ
EN£ģ
°ŗC°ųEMN=EM+MN+EN=![]() EN+
EN+![]() EN+EN=
EN+EN=![]() EN£ģ
EN£ģ
”…£®1£©÷™A£®0£¨2£©°ĘB£®4£¨0£©£¨…Ť÷ĪŌŖABĶńĹ‚őŲ Ĺő™£ļy=kx+2£¨
°ŗ4k+2=0£¨Ĺ‚Ķ√£ļk=![]() £¨
£¨
°ŗ÷ĪŌŖABĶńĹ‚őŲ Ĺő™£ļ![]() £ģ
£ģ
…ŤŇ◊őÔŌŖ…ŌĶ„EĶń◊ÝĪÍő™![]() £®0£ľt£ľ4£©£¨
£®0£ľt£ľ4£©£¨
°ŖEF°ÕOB£¨
°ŗŃÓy=![]() +2÷–x=t£¨y=
+2÷–x=t£¨y=![]() +2£¨
+2£¨
°ŗĶ„NĶń◊ÝĪÍő™£®t£¨©Ā![]() t+2£©£¨
t+2£©£¨
°ŗEN=©Ā![]() +t+4©Ā£®©Ā
+t+4©Ā£®©Ā![]() t+2£©=©Ā
t+2£©=©Ā![]() +
+![]() t+2£ģ
t+2£ģ
°ŗC°ųEMN=![]() £®©Ā
£®©Ā![]() +
+![]() t+2£©=©Ā
t+2£©=©Ā![]()
![]() £®0£ľt£ľ4£©£ģ
£®0£ľt£ľ4£©£ģ
°ŗĶĪ![]() Ī£¨EN◊Óīů£¨īň ĪC°ųEMN◊Óīů£¨
Ī£¨EN◊Óīů£¨īň ĪC°ųEMN◊Óīů£¨
°ŗC°ųEMN◊Óīůő™£ļ![]() [©Ā
[©Ā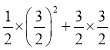 +2]=
+2]=![]() £ģ
£ģ
£®3£©”…£®2£©÷™£¨ĶĪC°ųEMN»°◊Óīů÷Ķ Ī£¨EFĶńĹ‚őŲ Ĺő™£ļx=![]() £ģ
£ģ
ĘŔ»Ű°ŌQDC=90°„£¨ĻżĶ„Q◊ųQG°Õy÷Š”ŕĶ„G£¨»ÁÕľ2ňý ĺ£ģ
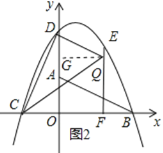
°ŖEFĶńĹ‚őŲ Ĺő™£ļx=![]() £¨
£¨
°ŗQG=![]() £¨
£¨
°Ŗ°ŌQDG+°ŌDQG=90°„£¨°ŌCDO+°ŌQDG=90°„£¨
°ŗ°ŌDGQ=°ŌCDO£¨
”÷°Ŗ°ŌQGD=°ŌDOC=90°„£¨
°ŗ°ųQDG°◊°ųDCO£¨
°ŗ![]() £¨
£¨
°ŗDG=2°Ń![]() £ģ
£ģ
°ŗOG=OD©ĀDG=4©Ā![]() £¨
£¨
°ŗĶ„QĶń◊ÝĪÍő™£®![]() £¨
£¨![]() £©£Ľ
£©£Ľ
Ęŕ»Ű°ŌDCQ=90°„£¨»ÁÕľ3ňý ĺ£ģ
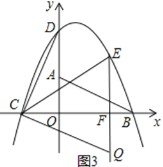
CF=![]() ©Ā£®©Ā2£©=
©Ā£®©Ā2£©=![]() £¨
£¨
°Ŗ°ŌQCF+°ŌOCD=90°„£¨°ŌCDO+°ŌOCD=90°„£¨
°ŗ°ŌQCF=°ŌCDO£¨
”÷°Ŗ°ŌCFQ=°ŌDOC=90°„£¨
°ŗ°ųCOD°◊°ųQFC£¨
°ŗ![]() £¨ľī
£¨ľī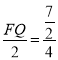 £¨
£¨
°ŗFQ=![]() £¨
£¨
°ŗĶ„QĶń◊ÝĪÍő™£®![]() £¨
£¨![]() £©£ģ
£©£ģ
◊Ř…Ōňý Ų£¨ĶĪĶ„QĶń◊ÝĪÍő™£®![]() £¨
£¨![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨
£¨![]() £© Ī£¨ ĻĶ√°ųQCD «“‘CDő™÷ĪĹ«ĪŖĶń÷ĪĹ«»żĹ«–ő£ģ
£© Ī£¨ ĻĶ√°ųQCD «“‘CDő™÷ĪĹ«ĪŖĶń÷ĪĹ«»żĹ«–ő£ģ

°ĺŐ‚ńŅ°Ņ“—÷™∂ĢīőļĮ ż![]() £¨
£¨![]() ”Ž
”Ž![]() Ķń≤Ņ∑÷∂‘”¶÷Ķ»ÁŌ¬ĪŪňý ĺ£ļ
Ķń≤Ņ∑÷∂‘”¶÷Ķ»ÁŌ¬ĪŪňý ĺ£ļ
| °≠ | -1 | 0 | 1 | 2 | 3 | 4 | °≠ |
| °≠ | 6 | 1 | -2 | -3 | -2 | m | °≠ |
Ō¬√ś”–ňńłŲ¬Ř∂Ō£ļ
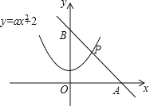
ĘŔŇ◊őÔŌŖ![]() Ķń∂•Ķ„ő™
Ķń∂•Ķ„ő™![]() £Ľ
£Ľ
Ęŕ![]() £Ľ
£Ľ
ĘŘĻō”ŕ![]() Ķń∑Ĺ≥Ő
Ķń∑Ĺ≥Ő![]() ĶńĹ‚ő™
ĶńĹ‚ő™![]() £Ľ
£Ľ
Ę‹![]() £ģ
£ģ
∆š÷–£¨’ż»∑Ķń”–___________________