题目内容
11.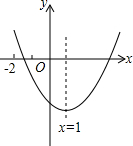 已知二次函数y=ax2+bx+c(a≠0)与x轴一个交点在-1,-2之间,对称轴为直线x=1,图象如图,给出以下结论:①b2-4ac>0;②abc>0;③2a-b=0;④8a+c<0;⑤$a+\frac{1}{3}b+\frac{1}{9}c$<0.其中结论正确的个数有( )
已知二次函数y=ax2+bx+c(a≠0)与x轴一个交点在-1,-2之间,对称轴为直线x=1,图象如图,给出以下结论:①b2-4ac>0;②abc>0;③2a-b=0;④8a+c<0;⑤$a+\frac{1}{3}b+\frac{1}{9}c$<0.其中结论正确的个数有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断即可.
解答 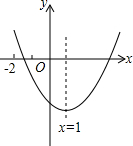 解:∵抛物线与x轴有两个交点,
解:∵抛物线与x轴有两个交点,
∴b2-4ac>0,①正确;
∵抛物线开口向上,
∴a>0,
∵对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,②正确;
∵-$\frac{b}{2a}$=1,∴2a+b=0,③错误;
∵x=-2时,y>0,
∴4a-2b+c>0,即8a+c>0,④错误;
根据抛物线的对称性可知,当x=3时,y<0,
∴9a+3b+c<0,
∴$a+\frac{1}{3}b+\frac{1}{9}c$<0,⑤正确.
综上所述,正确的结论是:①②⑤.
故选:C.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数y=ax2+bx+c系数符号与抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数的关系是解题的关键.

练习册系列答案
相关题目
3.计算(-2a)2的结果是( )
| A. | -4a2 | B. | 2a2 | C. | -2a2 | D. | 4a2 |
20.长春市轻轨3号线开通以来,极大缓解了城市的交通压力,据统计,每天轻轨的运载人数为16600人次,16600这个数用科学记数法表示为( )
| A. | 16.6×103 | B. | 1.66×104 | C. | 166×102 | D. | 1.66×105 |
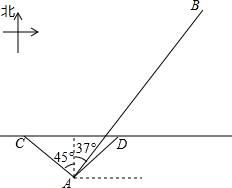 我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为$10\sqrt{2}$海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截.
我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为$10\sqrt{2}$海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截.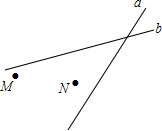 如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.
如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.