题目内容
【题目】如图，在
中，
，若点
从点
出发，以每秒
的速度沿折线
运动，设运动时间为
秒（
）．
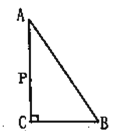
（1）用尺规作线段
的垂直平分线（不写作法，保留作图痕迹）；
（2）若点恰好运动到的垂直平分线上时，求的值．
【答案】（1）见解析；（2）
的值为
或
【解析】
(1)分别以AB为圆心,大于
AB为半径作弧,连接两户的交点即为线段AB的垂直平分线,
(2)勾股定理求出AC的长, 当P在AC上时,利用勾股定理解题,当P在AB上时,利用
解题.
解：（1）分别以AB为圆心,大于AB为半径作弧,连接两户的交点即为线段AB的垂直平分线,有作图痕迹；
（2）如图，在
中，由勾股定理得
，
①当P在AC上时,
，
∴
，
，
，
在
中，由勾股定理得：
即：
解得：
；
②当P在AB上时,
，
即：
，
∴
∴的值为或.
练习册系列答案
阅读快车系列答案
相关题目
