��Ŀ����
����Ŀ����ͼ����ֱ֪��lAC��y=��![]() ��x�ᡢy��ֱ�ΪA��C���㣬ֱ��BC��AC��x���ڵ�B��
��x�ᡢy��ֱ�ΪA��C���㣬ֱ��BC��AC��x���ڵ�B��
��1�����B�����꼰ֱ��BC�Ľ���ʽ��
��2������OBC����BC�߷��ۣ��õ���O��BC������O����ֱ��O��E��ֱx���ڵ�E��F��y����һ�㣬P��ֱ��O��E������һ�㣬P��Q�������x��Գƣ���|PA��PC|���ʱ�������QF+![]() FC����Сֵ��
FC����Сֵ��
��3����M��ֱ��O��E��һ�㣬��QM=3![]() ���ڣ�2���������£���ƽ��ֱ������ϵ�У��Ƿ���ڵ�N��ʹ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�
���ڣ�2���������£���ƽ��ֱ������ϵ�У��Ƿ���ڵ�N��ʹ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��B��6��0����y=![]() x��2
x��2![]() ����2��5
����2��5![]() ����3����6��3
����3����6��3![]() ����0��
����0��![]() ����0��7
����0��7![]() ������6��9
������6��9![]() ��.
��.
��������
��1�����ô���ϵ�������A��C�������꣬�ٸ�����ֱ�ߴ�ֱk�ij˻�Ϊ-1�����ֱ��BC�Ľ���ʽ���ɽ�����⣻
��2������֤����ACO=30�㣬��ͼ����QH��AC��H����y����F����FH=![]() CF�����ݴ��߶���̿�֪��QF+
CF�����ݴ��߶���̿�֪��QF+![]() FC����СֵΪ�߶�HQ�ij���
FC����СֵΪ�߶�HQ�ij���
��3�������M������������ηֱ�������⼴��.
�⣺��1��������A����2��0����C��0����2![]() ����
����
��ֱ��lAC��y=��![]() ��BC��AC��
��BC��AC��
��ֱ��BC�Ľ���ʽΪy=![]() x��2
x��2![]() ��
��
��y=0�����x=6��
��B��6��0����
��2���ߡ�OBC����BC�߷��ۣ��õ���O��BC��
��ɵ�O�䣨3����3![]() ����
����
��|PA��PC|���ʱ����P��ֱ��AC�ϣ���ʱP��3����5![]() ����
����
��P��Q����x��Գƣ�
��Q��3��5![]() ����
����
��Rt��AOC����tan��ACO=![]() =
=![]() ��
��
���ACO=30�㣬
��ͼ����QH��AC��H����y����F��
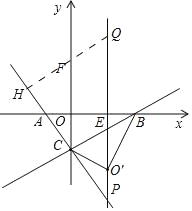
��FH=![]() CF��
CF��
���ݴ��߶���̿�֪��QF+![]() FC����СֵΪ�߶�HQ�ij���
FC����СֵΪ�߶�HQ�ij���
��Rt��PQH�У��ߡ�HPQ=��ACO=30�㣬PQ=10![]() ��
��
��HQ=![]() PQ=5
PQ=5![]() ��
��
��QF+![]() FC����СֵΪ5
FC����СֵΪ5![]() ��
��
��3���ɣ�2����֪��F��0��4![]() ����
����
��QM=3![]() ��
��
��M��3��2![]() ����3��8
����3��8![]() ����
����
��M��3��2![]() ��ʱ����ͼ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ��ɵ����������ĵ�N����Ϊ��6��3
��ʱ����ͼ����Q��F��M��N�ĵ�Ϊ������ı�����ƽ���ı��Σ��ɵ����������ĵ�N����Ϊ��6��3![]() ����0��
����0��![]() ����0��7
����0��7![]() ��,
��,
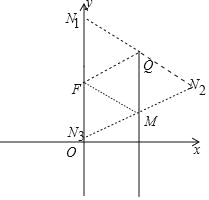
��MΪ��3��8![]() ��ʱ��ͬ���ɵ����������ĵ�N����Ϊ��6��9
��ʱ��ͬ���ɵ����������ĵ�N����Ϊ��6��9![]() ����0��7
����0��7![]() ����0��
����0��![]() ����
����

 ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д�




