题目内容
观察下列等式:
1×2=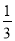 ×(1×2×3﹣0×1×2)
×(1×2×3﹣0×1×2)
2×3=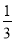 ×(2×3×4﹣1×2×3)
×(2×3×4﹣1×2×3)
3×4=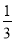 ×(3×4×5﹣2×3×4)
×(3×4×5﹣2×3×4)
…
计算:3×[1×2+2×3+3×4+…+n(n+1)]=_____.
n(n+1)(n+2) 【解析】试题解析:∵1×2=×(1×2×3-0×1×2) 2×3=×(2×3×4-1×2×3), 3×4=×(3×4×5-2×3×4), …, ∴n(n+1)= [n(n+1)(n+2)-(n-1)n(n+1)], ∴3×[1×2+2×3+3×4+…+n(n+1)] =3× [1×2×3-0×1×2+2×3×4-1×2×3+3×4×...
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目


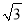 B. 18 C. 18
B. 18 C. 18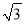 D. 36
D. 36
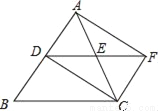
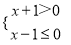 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )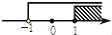 B.
B. 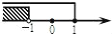
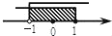 D.
D. 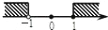
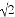 __2
__2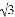 .
.