Question

【题目】△ABC中，∠C＝90°，AC＝3，BC＝4，将△ABC绕点C顺时针旋转a度(0°＜a＜180°)得到△DCE，点A与点D对应，点B与点E对应，当点D落在△ABC的边上时，则BD的长_______

Answer 1

【答案】或1

【解析】

根据题意画出图形，分点D在AB边上和BC边上两种情况讨论，当点D落在AB边上时，过点C作CH⊥AB于H，证△ACH∽△ABC，求出AD的长，可进一步求出BD的长；当点D落在BC边上时，由旋转知，AC＝CD＝3，所以BD＝BC﹣CD＝1．

解：在Rt△ABC中，AB＝＝＝5，

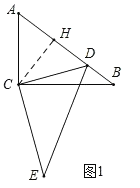
如图1，当点D落在AB边上时，

过点C作CH⊥AB于H，

由旋转知，AC＝CD＝3，

∴AH＝DH，

∵∠A＝∠A，∠AHC＝∠ACB＝90°，

∴△ACH∽△ABC，

∴，

∴＝，

∴AH＝，

∴AD＝2AH＝，

∴DB＝AB﹣AD＝5﹣＝；

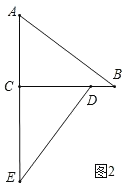
如图2，当点D落在BC边上时，

由旋转知，AC＝CD＝3，

∴BD＝BC﹣CD＝4﹣3＝1；

故答案为：或1．