Question

【题目】在平面直角坐标系xOy中，⊙C的半径为r(r＞1)，点P是圆内与圆心C不重合的点，⊙C的“完美点”的定义如下：过圆心C的任意直线CP与⊙C交于点A，B，若满足|PA﹣PB|＝2，则称点P为⊙C的“完美点”，如图点P为⊙C的一个“完美点”．

(1)当⊙O的半径为2时

①点M(，0)　 　⊙O的“完美点”，点(﹣，﹣)　 　⊙O的“完美点”；(填“是”或者“不是”)

②若⊙O的“完美点”P在直线y＝x上，求PO的长及点P的坐标；

(2)设圆心C的坐标为(s，t)，且在直线y＝﹣2x+1上，⊙C半径为r，若y轴上存在⊙C的“完美点”，求t的取值范围．

Answer 1

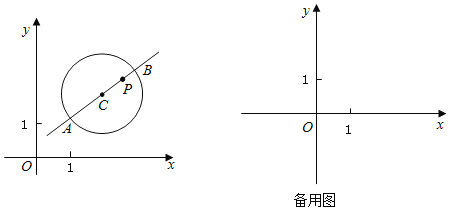
【答案】(1)①不是，是；②PO的长为1，点P的坐标为(，)或(﹣，﹣)；(2)t的取值范围为﹣1≤t≤3．

【解析】

（1）①利用圆的“完美点”的定义直接判断即可得出结论.②先确定出满足圆的“完美点”的OP的长度，然后分情况讨论计算即可得出结论；（2）先判断出圆的“完美点”的轨迹，然后确定出取极值时OC与y轴的位置关系即可得出结论.

解：(1)①∵点M(，0)，

∴设⊙O与x轴的交点为A，B，

∵⊙O的半径为2，

∴取A(﹣2，0)，B(2，0)，

∴|MA﹣MB|＝|(+2)﹣(2﹣)|＝3≠2，

∴点M不是⊙O的“完美点”，

同理：点(﹣，﹣)是⊙O的“完美点”．

故答案为不是，是．

②如图1，

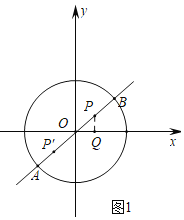
根据题意，|PA﹣PB|＝2，

∴|OP+2﹣(2﹣OP)|＝2，

∴OP＝1．

若点P在第一象限内，作PQ⊥x轴于点Q，

∵点P在直线y＝x上，OP＝1，

∴ ．

∴P( )．

若点P在第三象限内，根据对称性可知其坐标为(﹣，﹣)．

综上所述，PO的长为1，点P的坐标为()或（ ）)．

(2)对于⊙C的任意一个“完美点”P都有|PA﹣PB|＝2，

∴|CP+r﹣(r﹣CP)|＝2．

∴CP＝1．

∴对于任意的点P，满足CP＝1，都有|CP+r﹣(r﹣CP)|＝2，

∴|PA﹣PB|＝2，故此时点P为⊙C的“完美点”．

因此，⊙C的“完美点”是以点C为圆心，1为半径的圆．

设直线y＝﹣2x+1与y轴交于点D，如图2，

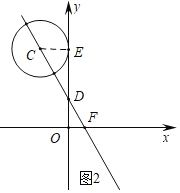
当⊙C移动到与y轴相切且切点在点D的上方时，t的值最大．

设切点为E，连接CE，

∵⊙C的圆心在直线y＝﹣2x+1上，

∴此直线和y轴，x轴的交点D(0，1)，F(，0)，

∴OF＝，OD＝1，

∵CE∥OF，

∴△DOF∽△DEC，

∴ ，

∴ ，

∴DE＝2，

∴OE＝3，

t的最大值为3，

当⊙C移动到与y轴相切且切点在点D的下方时，t的值最小．

同理可得t的最小值为﹣1．

综上所述，t的取值范围为﹣1≤t≤3．