题目内容
19. 如图在△ABC中,AD⊥BC于D点,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,BC=40cm,AD=30cm
如图在△ABC中,AD⊥BC于D点,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,BC=40cm,AD=30cm(1)求证:△AEH∽△ABC;
(2)求正方形EFGH的边长.
分析 (1)根据EH∥BC即可证明.
(2)如图设AD与EH交于点M,首先证明四边形EFDM是矩形,设正方形边长为x,再利用△AEH∽△ABC,得$\frac{EH}{BC}$=$\frac{AO}{AD}$,列出方程即可解决问题.
解答 (1)证明:∵四边形EFGH是正方形,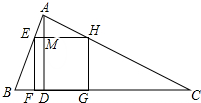
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC.
(2)解:
∵∠EFD=∠FEO=∠FDO=90°,
∴四边形EFDO是矩形,
∴EF=DO,设正方形EFGH的边长为x,
∵△AEH∽△ABC,
∴$\frac{EH}{BC}$=$\frac{AO}{AD}$,
∴$\frac{x}{40}$=$\frac{30-x}{30}$,
∴x=$\frac{120}{7}$,
∴正方形EFGH的边长为$\frac{120}{7}$cm.
点评 本题考查正方形的性质、相似三角形的判定和性质等知识,解题的关键是利用相似三角形的相似比对于高的比,学会用方程的思想解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%.某人于2007年6月5日存入定期为1年的人民币5 000元(到期后银行将扣除20%的利息税).设到期后银行应向储户支付现金x元,则所列方程正确的是( )
| A. | x-5 000=5 000×3.06% | |
| B. | x+5 000×20%=5 000×(1+3.06%) | |
| C. | x+5 000×3.06%×20%=5 000×(1+3.06%) | |
| D. | x+5 000×3.06%×20%=5 000×3.06% |
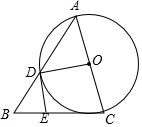 已知:如图,在△ABC中,AC=BC,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
已知:如图,在△ABC中,AC=BC,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;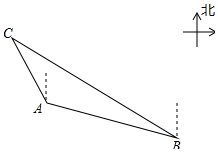 如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为16海里.求A、C两地之间的距离.(保留根号)
如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为16海里.求A、C两地之间的距离.(保留根号) 能展开成如图所示的几何体名称是三棱柱.
能展开成如图所示的几何体名称是三棱柱.