题目内容
10.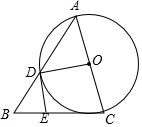 已知:如图,在△ABC中,AC=BC,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
已知:如图,在△ABC中,AC=BC,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.(1)求证:DE⊥BC;
(2)若⊙O的半径为5,cosB=$\frac{3}{5}$,求AB的长.
分析 (1)连接OD,由AC是⊙O的直径,得到CD⊥AB,根据等腰三角形的性质得到AD=BD,根据切线的性质即可得到结论;
(2)根据等腰三角形的性质得到∠A=∠B,解直角三角形得到AC=10,于是得到结论.
解答 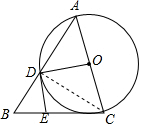 解:(1)连接OD,
解:(1)连接OD,
∵AC是⊙O的直径,
∴CD⊥AB,
∵AC=BC,
∴AD=BD,
∵AO=CO,
∴OD∥BC,
∵DE是⊙O的切线,
∴OD⊥DE,
∴DE⊥BC;
(2)∵AC=BC,
∴∠A=∠B,
∵cosB=$\frac{3}{5}$,
∴cosA=$\frac{3}{5}$,
∵⊙O的半径为5,
∴AC=10,
∴AD=6,
∴AB=2AD=12.
点评 此题考查了切线的性质,等腰三角形的判定与性质,圆周角定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
相关题目
5. 如图,在△ABC中,∠ABC=90°,∠A=30°,BC=1.M、N分别是AB、AC上的任意一点,求MN+NB的最小值为( )
如图,在△ABC中,∠ABC=90°,∠A=30°,BC=1.M、N分别是AB、AC上的任意一点,求MN+NB的最小值为( )
 如图,在△ABC中,∠ABC=90°,∠A=30°,BC=1.M、N分别是AB、AC上的任意一点,求MN+NB的最小值为( )
如图,在△ABC中,∠ABC=90°,∠A=30°,BC=1.M、N分别是AB、AC上的任意一点,求MN+NB的最小值为( )| A. | 1.5 | B. | 2 | C. | $\frac{{\sqrt{3}}}{2}$+$\frac{3}{4}$ | D. | $\sqrt{3}$ |
2.下列说法不正确的是( )
| A. | 0的平方根是0 | B. | 40的算术平方根是20 | ||
| C. | -1的立方根是-1 | D. | $\sqrt{10}$是10的平方根 |

 如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=100°,求∠EBC=40度.
如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=100°,求∠EBC=40度. 如图在△ABC中,AD⊥BC于D点,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,BC=40cm,AD=30cm
如图在△ABC中,AD⊥BC于D点,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,BC=40cm,AD=30cm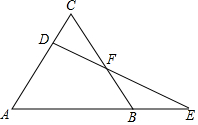 如图,已知△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连结DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连结DE交BC于F.