题目内容
14.若一个三角形的三个顶点均在一个图形的不同的边上,则称此三角形为该图形的内接三角形.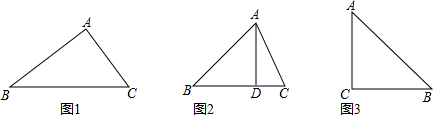
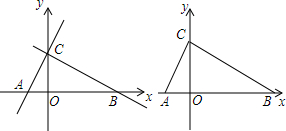
(1)在图1中画出△ABC的一个内接直角三角形;
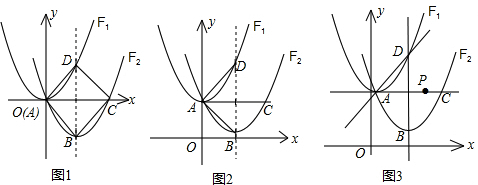
(2)如图2,已知△ABC中,∠BAC=60°,∠B=45°,AB=8,AD为BC边上的高,探究以D为一个顶点作△ABC的内接三角形,其周长是否存在最小值?若存在,请求出最小值;若不存在,请说明理由;
(3)如图3,△ABC为等腰直角三角形,∠C=90°,AC=6,试探究:△ABC的内接等腰直角三角形的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
分析 (1)利用已知内接三角形的定义结合直角三角形作法得出答案;
(2)分别作点D关于AB、AC的轴对称点D′、D″,连接D′D″,交AB、AC于点E、F,连接DE、DF,则△DEF即为周长最小的内接三角形,再利用已知结合锐角三角函数关系得出HD″=AD″•cos30°,即可得出答案;
(3)利用分类讨论①当内接等腰直角三角形的直角顶点在斜边AB上时,②当内接等腰直角三角形的直角顶点在直角边上时,分别得出答案.
解答 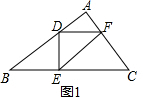 解:(1)如图1,△DEF为所求作的三角形(答案不唯一);
解:(1)如图1,△DEF为所求作的三角形(答案不唯一);
(2)存在.
如图2,分别作点D关于AB、AC的轴对称点D′、D″,连接D′D″,交AB、AC于点E、F,
连接DE、DF,则△DEF即为周长最小的内接三角形,
D′D″的长即为最小周长.
∵AB=8,∠B=45°,AD⊥BC,
∴AD=AB•sin45°=4$\sqrt{2}$.
∵点D关于AB、AC的轴对称点分别为D′、D″,
∴AD′=AD″=AD=4$\sqrt{2}$,∠D′AD″=2∠BAC=120°,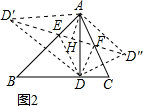
过点A作AH⊥EF于点H,
在Rt△AHD″中,∠AD″H=30°,
∴HD″=AD″•cos30°=2$\sqrt{6}$,
∴△DEF周长的最小值为4$\sqrt{6}$;
(3)分类讨论:
①当内接等腰直角三角形的直角顶点在斜边AB上时,
如图3,∵∠ACB=∠EDF=90°,
以EF为直径画圆,则点C、D在圆上,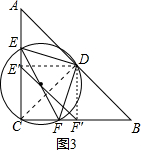
连接CD,∵DE=DF,
∴∠ACD=∠BCD,
又∵AC=BC,
∴CD是AB边上的中线,点D是AB边的中点,
过点D作DE′⊥AC,DF′⊥BC,此时,DE′、DF′最短.
当点E与E′重合,点F与F′重合时,△DEF的面积最小,
此时四边形CEDF为矩形.
设DE=x,则BC=2DE=2x=6,
∴x=3,∴S最小=$\frac{9}{2}$;
②当内接等腰直角三角形的直角顶点在直角边上时,如图4,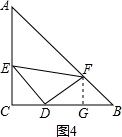
过点F作FG⊥BC于点G,设DG=y,GF=x,
∵∠EDF=90°,
∴∠EDC+∠FDG=90°,
∵∠CED+∠EDC=90°,
∴∠CED=∠FDG,
在△CDE和△GFD中
$\left\{\begin{array}{l}{∠C=∠FGD}\\{∠CED=∠GDF}\\{ED=DF}\end{array}\right.$,
∴△CDE≌△GFD(AAS),
∴CD=FG=x,
∵∠B=45°,FG⊥BC,
∴GB=GF=x,
∴BC=CD+DG+GB=2x+y=6,即y=6-2x.
S△DEF=$\frac{1}{2}$DF2=$\frac{1}{2}$(y2+x2)
=$\frac{5}{2}$x2-12x+18
=$\frac{5}{2}$(x-$\frac{12}{5}$)2+$\frac{18}{5}$,
故当x=$\frac{12}{5}$时,S最小=$\frac{18}{5}$,
∵$\frac{9}{2}$>$\frac{18}{5}$,
∴△DEF的面积存在最小值,其最小值为$\frac{18}{5}$.
点评 此题主要考查了圆的综合以及全等三角形的判定与性质和二次函数最值求法、等腰直角三角形的性质、锐角三角函数关系等知识,利用分类讨论、数形结合得出三角形的面积的最小值是解题关键.

| A. | 1个 | B. | 2个 | C. | 4个 | D. | 8个 |
 如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )
如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )| A. | 65° | B. | 75° | C. | 85° | D. | 不能确定 |
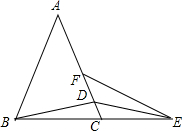 如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.