题目内容
 在△ABC中,∠B=60°,∠BCA=20°,∠DAC=20°,∠BCA的平分线交AB于E,连DE,则∠BDE=
在△ABC中,∠B=60°,∠BCA=20°,∠DAC=20°,∠BCA的平分线交AB于E,连DE,则∠BDE=考点:三角形内角和定理,四点共圆,角平分线的定义,角的计算,三角形的外角性质
专题:
分析:利用过D点作AC的垂直平分线,交CE于F点,连接AF,得出∠6=∠7=70°,进而得出A、E、D、F四点共圆得出答案即可.
解答: 解:过D点作AC的垂直平分线,交CE于F点,连接AF,
解:过D点作AC的垂直平分线,交CE于F点,连接AF,
∵∠BCA=20°,∠DAC=20°,∠BCA的平分线交AB于E,
∴∠1=∠2=∠3=∠4=10°,
∵∠B=60°,∠ADB=∠BCA+∠DAC=40°,
∴∠6=∠7=70°,
所以A、E、D、F四点共圆,
∴∠5=∠4=10°,
∴所求的∠BDE=∠2+∠5=20°.
故答案为:20°.
 解:过D点作AC的垂直平分线,交CE于F点,连接AF,
解:过D点作AC的垂直平分线,交CE于F点,连接AF,∵∠BCA=20°,∠DAC=20°,∠BCA的平分线交AB于E,
∴∠1=∠2=∠3=∠4=10°,
∵∠B=60°,∠ADB=∠BCA+∠DAC=40°,
∴∠6=∠7=70°,
所以A、E、D、F四点共圆,
∴∠5=∠4=10°,
∴所求的∠BDE=∠2+∠5=20°.
故答案为:20°.
点评:此题主要考查了角平分线的性质以及四点共圆的性质,根据已知得出A、E、D、F四点共圆是解题关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
批发部经营某种商品,批发价(销售价)每只500元,毛利率为4%,该库存商品资金有80%向银行借贷,月利率为4.2‰,商品的保管经营费每只每天0.30元,则不发生亏本时商品的平均储存期最多为( )
| A、53天 | B、54天 |
| C、55天 | D、56天 |
 已知抛物线y=ax2+bx+c如图所示,则下列结论中,正确的是( )
已知抛物线y=ax2+bx+c如图所示,则下列结论中,正确的是( )| A、a>0 |
| B、a-b+c>0 |
| C、b2-4ac<0 |
| D、2a+b=0 |
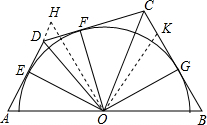 如图:设凸四边形ABCD的顶点在同一个圆上,另一个圆的圆心O在边AB上,且与四边形的其余的三条边相切,求证:AD+BC=AB.
如图:设凸四边形ABCD的顶点在同一个圆上,另一个圆的圆心O在边AB上,且与四边形的其余的三条边相切,求证:AD+BC=AB.