题目内容
20.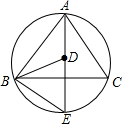 如图,AE平分∠BAC,交△ABC的外接圆于点E,D是AE上一点,且ED=EB,点D是否是△ABC的内心?为什么?
如图,AE平分∠BAC,交△ABC的外接圆于点E,D是AE上一点,且ED=EB,点D是否是△ABC的内心?为什么?
分析 根据题意得到∠BAE=∠CAE,根据等腰三角形的性质得到∠EBD=∠EDB,根据三角形外角的性质和圆周角定理得到∠ABD=∠DBC,根据内心的概念得到答案.
解答 解:点D是△ABC的内心,
证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵ED=EB,∴∠EBD=∠EDB,
∵∠EBD=∠EBC+∠DBC,∠EDB=∠BAE+∠ABD,又∠EBC=∠EAC=∠ABE,
∴∠ABD=∠DBC,
∴BD是∠ABC的平分线,又AE平分∠BAC,
∴点D是△ABC的内心.
点评 本题考查的是三角形的内切圆和内心、三角形的外角的性质以及圆周角定理,掌握三角形的内心是三角形三条角平分线的交点和同弧所对的圆周角相等是解题的关键.

练习册系列答案
相关题目
15.数-3,0,$\frac{1}{2}$,-5的大小顺序是( )
| A. | -5<-3<$\frac{1}{2}$<0 | B. | 13<-5<$\frac{1}{2}$<0 | C. | -3<-5<0<$\frac{1}{2}$ | D. | -5<-3<0<$\frac{1}{2}$ |
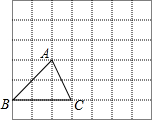 如图,已知三角形ABC,请根据下列提示作图:
如图,已知三角形ABC,请根据下列提示作图: