Question

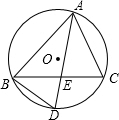如图，△ABC内接于⊙O，I为△ABC的角的平分线交点，延长AI分别交⊙O、BC于D、E两点．
（1）求证：DI=DB；
（2）试判断△ABC为什么三角形时，四边形BDCI为菱形？说明你的理由．

Answer 1

考点：菱形的判定,圆周角定理

专题：

分析：（1）连接BI，根据三角形的内切圆的定义求出∠ABI=∠CBI，∠BAD=∠CAD=∠DBC，求出∠DIB=∠IBD即可；
（2）根据等边三角形的性质得出∠BAC=∠ABC=∠ACB=60°，求出O和I重合，求出△BID和△DIC是等边三角形，得出IB=BD=DC=IC，根据菱形的判定得出即可．

解答：（1）证明：连接BI，
∵I是△ABC的内切圆的圆心，
∴∠ABI=∠CBI，∠BAD=∠CAD=∠DBC，
∵∠BID=∠BAD+∠ABI，∠IBD=∠CBI+∠DBC，
∴∠DIB=∠IBD，
∴DI=DB；

（2）解：当△ABC时等边三角形时，四边形BDCI为菱形，
理由是：∵△ABC是等边三角形，
∴∠BAC=∠ABC=∠ACB=60°，
∴∠ADB=∠ACB=60°，
∵⊙O和⊙I是等边三角形的外接圆和内切圆，
∴O和I重合，
∴由（1）知：BD=DI（即BD=DO），
∴△BID是等边三角形，
同理△DIC是等边三角形，
∴IB=BD=DC=IC，
∴四边形BDCI是菱形
即△ABC为等边三角形时，四边形BDCI为菱形．

点评：本题考查了三角形的内切圆和外接圆，三角形外角性质，菱形的判定，等边三角形的性质和判定的应用，主要考查学生综合运用性质进行推理的能力，题目有一定的难度．