题目内容
九(三)班在“2012年新春联欢会”中,开设了一个摸奖游戏,规则如下:有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、2张哭脸.现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.若正面是笑脸的就获奖,正面是哭脸的不获奖.
(1)若你有一次翻牌机会,从中随机翻开一张纸牌,获奖的概率是 .
(2)在某个游戏环节中,甲、乙两同学恰好同时都有一次翻牌的机会.这时甲同学要求先翻牌,认为这样获奖的可能大,你认为先、后翻牌获奖的可能性一样吗?请你用列表法或树状图利用所学知识加以说明.
(1)若你有一次翻牌机会,从中随机翻开一张纸牌,获奖的概率是
(2)在某个游戏环节中,甲、乙两同学恰好同时都有一次翻牌的机会.这时甲同学要求先翻牌,认为这样获奖的可能大,你认为先、后翻牌获奖的可能性一样吗?请你用列表法或树状图利用所学知识加以说明.
考点:列表法与树状图法,概率公式
专题:
分析:(1)根据正面有2张笑脸、2张哭脸,而翻一次牌正面是笑脸的就获奖,直接的出获胜概率.
(2)运用图表列举出所有可能即可得出分别获胜的概率.
(2)运用图表列举出所有可能即可得出分别获胜的概率.
解答:解:(1)∵有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、2张哭脸,翻一次牌正面是笑脸的就获奖,正面是哭脸的不获奖,
∴获奖的概率是
(或填0.5).
故答案为:
(或填0.5).
(2)他们获奖机会不相等,理由如下:
甲:
∴P(甲获奖)=
;
乙:
P(乙获奖)=
,
因为
≠
,所以他们获奖的机会不相等.
∴获奖的概率是
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
(2)他们获奖机会不相等,理由如下:
甲:
第一张 第 二张 | 笑1 | 笑2 | 哭1 | 哭2 |
| 笑1 | 笑1,笑1 | 笑2,笑1 | 哭1,笑1 | 哭2,笑1 |
| 笑2 | 笑1,笑2 | 笑2,笑2 | 哭1,笑2 | 哭2,笑2 |
| 哭1 | 笑1,哭1 | 笑2,哭1 | 哭1,哭1 | 哭2,哭1 |
| 哭2 | 笑1,哭2 | 笑2,哭2 | 哭1,哭2 | 哭2,哭2 |
| 1 |
| 4 |
乙:
第一张 第 二张 | 笑1 | 笑2 | 哭1 | 哭2 |
| 笑1 | 笑2,笑1 | 哭1,笑1 | 哭2,笑1 | |
| 笑2 | 笑1,笑2 | 哭1,笑2 | 哭2,笑2 | |
| 哭1 | 笑1,哭1 | 笑2,哭1 | 哭2,哭1 | |
| 哭2 | 笑1,哭2 | 笑2,哭2 | 哭1,哭2 |
| 1 |
| 6 |
因为
| 1 |
| 4 |
| 1 |
| 6 |
点评:此题主要考查了列举法求概率,列举出事件中所有的结果是解决问题的关键.

练习册系列答案
相关题目
若2xy2m+6z-2x2y+4yz+1是六次四项式,则m的值为( )
| A、-2 | ||
| B、-1 | ||
C、-
| ||
| D、7 |
给出下列各数:-3,0,+5,-3
,+3.1,-
,2004,+2010;其中是负数的有 ( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,已知EF是梯形ABCD的中位线,△AEF的面积为4cm2,则梯形ABCD的面积为
如图,已知EF是梯形ABCD的中位线,△AEF的面积为4cm2,则梯形ABCD的面积为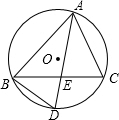 如图,△ABC内接于⊙O,I为△ABC的角的平分线交点,延长AI分别交⊙O、BC于D、E两点.
如图,△ABC内接于⊙O,I为△ABC的角的平分线交点,延长AI分别交⊙O、BC于D、E两点.