��Ŀ����
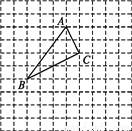
��ͼ��ʾ,��ABC��������������,��A������Ϊ(0,4),��Ҫ������������:
(1)��ͼ�н�����ȷ��ƽ��ֱ������ϵ,��д����B,C������;
(2)������A'B'C'����x��ĶԳ�ͼ��.(��д����)
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ��ʾ,��ABC��������������,��A������Ϊ(0,4),��Ҫ������������:
(1)��ͼ�н�����ȷ��ƽ��ֱ������ϵ,��д����B,C������;
(2)������A'B'C'����x��ĶԳ�ͼ��.(��д����)
