题目内容
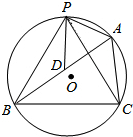 如图,△ABC内接于⊙O,D是AB边上一点,AB=6,AC=BD=4,P是优弧BAC的中点,连接PA、PB、PC、PD,若PB=
如图,△ABC内接于⊙O,D是AB边上一点,AB=6,AC=BD=4,P是优弧BAC的中点,连接PA、PB、PC、PD,若PB=| 29 |
考点:全等三角形的判定与性质,勾股定理,圆周角定理
专题:
分析:证△PBD≌△PCA,推出PA=PD,求出AM=DM=1,根据勾股定理求出PM,再根据勾股定理求出PA即可.
解答: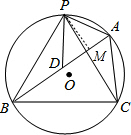
解:过P作PM⊥AB于M,
∵P为弧BAC的中点,
∴PB=PC,
∵弧PA对圆周角∠PBD和∠PCA,
∴∠PBD=∠PCA,
在△PBD和△PCA中
∴△PBD≌△PCA,
∴PD=PA,
∵PM⊥AB,
∴DM=AM,
∵AB=6,BD=4,
∴AD=2,
∴DM=AM=1,
在Rt△PMB中,PM=
=
=2,
在Rt△PMA中,由勾股定理得:PA=
=
=
.

解:过P作PM⊥AB于M,
∵P为弧BAC的中点,
∴PB=PC,
∵弧PA对圆周角∠PBD和∠PCA,
∴∠PBD=∠PCA,
在△PBD和△PCA中
|
∴△PBD≌△PCA,
∴PD=PA,
∵PM⊥AB,
∴DM=AM,
∵AB=6,BD=4,
∴AD=2,
∴DM=AM=1,
在Rt△PMB中,PM=
| PB2-BM2 |
(
|
在Rt△PMA中,由勾股定理得:PA=
| PM2+AM2 |
| 22+12 |
| 5 |
点评:本题考查了圆心角、弧、弦之间的关系,勾股定理,全等三角形的性质和判定,等腰三角形的应用,题目比较典型,综合性比较强.

练习册系列答案
相关题目
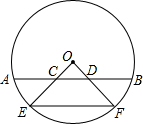 在⊙O中,弦AB∥EF,连结OE、OF交AB于C、D,求证:AC=DB.
在⊙O中,弦AB∥EF,连结OE、OF交AB于C、D,求证:AC=DB.