题目内容
对于二次函数y=ax2-(2a-1)x+a-1(a≠0),有下列结论:
①其图象与x轴一定相交;
②若a<0,函数在x>1时,y随x的增大而减小;
③无论a取何值,抛物线的顶点始终在同一条直线上;
④无论a取何值,函数图象都经过同一个点.
其中所有正确的结论是 .(填写正确结论的序号)
①其图象与x轴一定相交;
②若a<0,函数在x>1时,y随x的增大而减小;
③无论a取何值,抛物线的顶点始终在同一条直线上;
④无论a取何值,函数图象都经过同一个点.
其中所有正确的结论是
考点:二次函数的性质
专题:
分析:令y=0,解方程求出抛物线与x轴的两个交点坐标,从而判断出①④正确,利用抛物线的顶点坐标列式整理,再根据二次函数的增减性判断出②错误;消掉a即可得到顶点所在的直线,判断出③正确.
解答:解:令y=0,则ax2-(2a-1)x+a-1=0,
解得x1=1,x2=
,
所以,函数图象与x轴的交点为(1,0),(
,0),故①④正确;
当a<0时,
>1,
所以,函数在x>1时,y先随x的增大然后再减小,故②错误;
∵x=-
=-
=1-
,
y=
=
=-
,
∴y=
x-
,
即无论a取何值,抛物线的顶点始终在直线y=
x-
上,故③正确;
综上所述,正确的结论是①③④.
故答案为:①③④.
解得x1=1,x2=
| a-1 |
| a |
所以,函数图象与x轴的交点为(1,0),(
| a-1 |
| a |
当a<0时,
| a-1 |
| a |
所以,函数在x>1时,y先随x的增大然后再减小,故②错误;
∵x=-
| b |
| 2a |
| -(2a-1) |
| 2a |
| 1 |
| 2a |
y=
| 4ac-b2 |
| 4a |
| 4a(a-1)-(2a-1)2 |
| 4a |
| 1 |
| 4a |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
即无论a取何值,抛物线的顶点始终在直线y=
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,正确的结论是①③④.
故答案为:①③④.
点评:本题考查了二次函数的性质,主要利用了二次函数的与x轴的交点,二次函数的增减性,顶点坐标,难点在于利用a表示出顶点的横坐标与纵坐标,然后消掉a得到顶点所在的直线.

练习册系列答案
相关题目
 如图所示,AB=AD,AC=AE,∠DAB=∠CAE,BE与DC交于点P.求证:PA平分∠DPE.
如图所示,AB=AD,AC=AE,∠DAB=∠CAE,BE与DC交于点P.求证:PA平分∠DPE.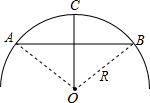 如图,在残破的圆形的轮片图中,弦AB=24cm,半径OC⊥AB于D,CD=4cm,求原轮片的直径.
如图,在残破的圆形的轮片图中,弦AB=24cm,半径OC⊥AB于D,CD=4cm,求原轮片的直径. 如图,矩形ABCD中,对角线AC、BD相交于点O,AC=6,则OD=
如图,矩形ABCD中,对角线AC、BD相交于点O,AC=6,则OD=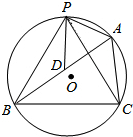 如图,△ABC内接于⊙O,D是AB边上一点,AB=6,AC=BD=4,P是优弧BAC的中点,连接PA、PB、PC、PD,若PB=
如图,△ABC内接于⊙O,D是AB边上一点,AB=6,AC=BD=4,P是优弧BAC的中点,连接PA、PB、PC、PD,若PB=