题目内容
15. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E,若AD=BE,则△A′DE的面积是$\frac{3}{2}$.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E,若AD=BE,则△A′DE的面积是$\frac{3}{2}$.
分析 在Rt△ABC中,由勾股定理求得AB=5,由旋转的性质可知AD=A′D,设AD=A′D=BE=x,则DE=5-2x,根据旋转90°可证△A′DE∽△ACB,利用相似比求x,再求△A′DE的面积.
解答 解:Rt△ABC中,由勾股定理求AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
由旋转的性质,设AD=A′D=BE=x,则DE=5-2x,
∵△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,
∴∠A′=∠A,∠A′DE=∠C=90°,
∴△A′DE∽△ACB,
∴$\frac{DE}{A'D}$=$\frac{BC}{AC}$,即$\frac{5-2x}{x}$=$\frac{4}{3}$,解得x=$\frac{3}{2}$,
∴S△A′DE=$\frac{1}{2}$DE×A′D=$\frac{1}{2}$×(5-2×$\frac{3}{2}$)×$\frac{3}{2}$=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查了相似三角形的判定与性质,勾股定理及旋转的性质.关键是根据旋转的性质得出相似三角形,利用相似比求解.

练习册系列答案
相关题目
6.下列调查中,适合采用全面调查的是( )
| A. | 了解我国各地中学多媒体的使用情况 | |
| B. | 测试我国某新型导弹的威力 | |
| C. | 对某商场防火安全的调查 | |
| D. | 对今年全国各地酒店“杜绝浪费,提倡节约”的调查 |
 如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点,则EF+BF的最小值为$\sqrt{3}$.
如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点,则EF+BF的最小值为$\sqrt{3}$. 如图,△ABC中,AB=6,BC=8,tan∠B=$\frac{4}{3}$,点D是边BC上的一个动点(点D与点B不重合),过点D作DE⊥AB,垂足为E,点F是AD的中点,连接EF,设△AEF的面积为y,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是( )
如图,△ABC中,AB=6,BC=8,tan∠B=$\frac{4}{3}$,点D是边BC上的一个动点(点D与点B不重合),过点D作DE⊥AB,垂足为E,点F是AD的中点,连接EF,设△AEF的面积为y,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是( )



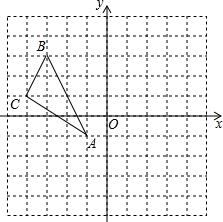 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1)
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1) 是
是  的弦,
的弦,  是
是  的切线,
的切线,  为切点,
为切点,  经过圆心,若
经过圆心,若  ,则
,则  的大小等于( )
的大小等于( ) 
 B.
B. 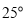 C.
C.  D.
D. 