题目内容
3.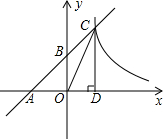 如图,已知一次函数y=kx+b(k≠0)的图象分别与x轴、y轴相交于A、B两点,并且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于第一象限内的一点C,线段CD⊥x轴于点D,OA=OB=OD=1.
如图,已知一次函数y=kx+b(k≠0)的图象分别与x轴、y轴相交于A、B两点,并且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于第一象限内的一点C,线段CD⊥x轴于点D,OA=OB=OD=1.(1)请直接写出A、B、D三点的坐标.
(2)求一次函数与反比例函数的表达式.
(3)连接OC,求△AOC的面积.
分析 (1)根据OA=OB=OD=1即可得出A、B、D的坐标;
(2)利用待定系数法即可求出函数解析式;
(3)根据A、C的坐标,利用三角形面积公式即可求得.
解答 解:(1)∵OA=OB=OD=1,
∴A(-1,0),B(0,1),D(1,0).
(2)设一次函数解析式为y=kx+b,把A(-1,0),B(0,1)分别代入解析式得,
$\left\{\begin{array}{l}{-k+b=0}\\{b=1}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴一次函数即AB解析式为y=x+1,
当x=1时,y=2,即C(1,2),
∴反比例函数解析式:y=$\frac{2}{x}$.
(3)∵A(-1,0),C(1,2),
∴S△AOC=$\frac{1}{2}$OA•yC=$\frac{1}{2}$×1×2=1.
点评 此题是一道反比例函数综合题,涉及待定系数法、一次函数与反比例函数的交点问题、及三角形的面积等.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
14.已知A、B两点在数轴上,若点A对应的数为2,线段AB的长为3,则点B对应的数为( )
| A. | 5 | B. | -1或5 | C. | ±5 | D. | ±1 |
11.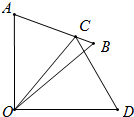 如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,
如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,
且∠AOD的度数为90°,则∠B的度数是( )
 如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,
如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是( )
| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
18.已知二次函数y=x2+2x-3,关于这个二次函数的图象有如下说法:
①图象的开口一定向上;②图象的顶点一定在第四象限;③图象与x轴的交点有一个在y轴的右侧.
以上说法正确的个数为( )
①图象的开口一定向上;②图象的顶点一定在第四象限;③图象与x轴的交点有一个在y轴的右侧.
以上说法正确的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
8.已知(-0.5,y1),(-1,y2),(0.5,y3)是直线y=-2x+b(b为常数)上的三点,则y1,y2,y3的大小关系是( )
| A. | y3<y1<y2 | B. | y1<y2<y3 | C. | y2<y3<y1 | D. | y2<y1<y3 |
 如图,直线上有三个正方形a,b.c,若a,c的面积分别为5和12,则b的面积为17.
如图,直线上有三个正方形a,b.c,若a,c的面积分别为5和12,则b的面积为17.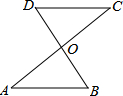 如图,AC和BD相交于点O,OA=OC,OB=OD,求证:AB∥CD.
如图,AC和BD相交于点O,OA=OC,OB=OD,求证:AB∥CD.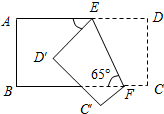 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′和∠BFC′的度数.
如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′和∠BFC′的度数.