题目内容
11.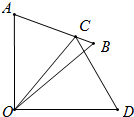 如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,
如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是( )
| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
分析 如图,首先求出∠A的度数,进而求出∠BOC的度数,运用三角形的内角和定理即可解决问题.
解答  解:如图,由旋转变换的性质得:∠AOC=∠BOD=40°,OA=OC,
解:如图,由旋转变换的性质得:∠AOC=∠BOD=40°,OA=OC,
∴∠A=∠ACO=$\frac{180°-40°}{2}$=70°;
∵∠AOD=90°,
∴∠BOC=90°-80°=10°,∠AOB=50°;
∴∠B=180°-70°-50°=60°,
故选B.
点评 该题主要考查了旋转变换的性质、等腰三角形的性质、三角形的内角和定理等几何知识点及其应用问题;牢固掌握旋转变换的性质、等腰三角形的性质等几何知识点是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
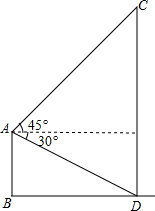 如图,平地上一个建筑物AB与铁塔CD相距60m,在建筑物的顶部测得铁塔底部的俯角为30°,测得铁塔顶部的仰角为45°,求铁塔的高度($\sqrt{3}$取1.732,精确到1m).
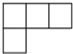
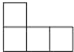
如图,平地上一个建筑物AB与铁塔CD相距60m,在建筑物的顶部测得铁塔底部的俯角为30°,测得铁塔顶部的仰角为45°,求铁塔的高度($\sqrt{3}$取1.732,精确到1m).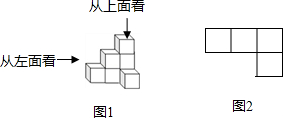 我们从不同的方向观察同一个物体时,可以看到不同的平面图,图1是由若干个小正方体所搭成的立体图形,图2是从图1的上面看这个立体图形时所看到的平面图,那么从图1的左面看这个立体图形,所看到的平面图是( )
我们从不同的方向观察同一个物体时,可以看到不同的平面图,图1是由若干个小正方体所搭成的立体图形,图2是从图1的上面看这个立体图形时所看到的平面图,那么从图1的左面看这个立体图形,所看到的平面图是( )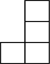

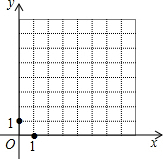 如图,在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.平移1次后,可能到达的点的坐标是(0,2)、(1,0),这些点在函数y=-2x+2的图象上;平移2次后,可能到达的点的坐标是(0,4)、(1,2)、(2,0),这些点在函数y=-2x+4的图象上;平移3次后,可能到达的点的坐标是(0,6)、(1,4)、(2,2)、(3,0),这些点在函数y=-2x+6的图象上.
如图,在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.平移1次后,可能到达的点的坐标是(0,2)、(1,0),这些点在函数y=-2x+2的图象上;平移2次后,可能到达的点的坐标是(0,4)、(1,2)、(2,0),这些点在函数y=-2x+4的图象上;平移3次后,可能到达的点的坐标是(0,6)、(1,4)、(2,2)、(3,0),这些点在函数y=-2x+6的图象上.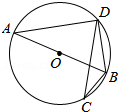 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD=40°.
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD=40°.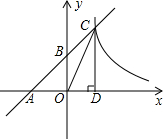 如图,已知一次函数y=kx+b(k≠0)的图象分别与x轴、y轴相交于A、B两点,并且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于第一象限内的一点C,线段CD⊥x轴于点D,OA=OB=OD=1.
如图,已知一次函数y=kx+b(k≠0)的图象分别与x轴、y轴相交于A、B两点,并且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于第一象限内的一点C,线段CD⊥x轴于点D,OA=OB=OD=1.
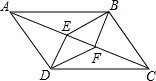 如图,?ABCD中,DE⊥AC,BF⊥AC,垂足分别为E、F,求证:BE∥DF.
如图,?ABCD中,DE⊥AC,BF⊥AC,垂足分别为E、F,求证:BE∥DF.