题目内容
 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,则阴影部分的面积为
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,则阴影部分的面积为考点:切线的性质,勾股定理,垂径定理
专题:
分析:如图,作OE⊥MN于E.根据切线的性质得O1D为⊙O1的半径,易得四边形OO1DC为矩形,则OC=O1D,再根据垂径定理得到AC=BC=
MN,在Rt△OEN中,利用勾股定理得到ON2-OE2=EN2=
a2,然后利用阴影部分的面积=
S⊙C-
S⊙O进行计算.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: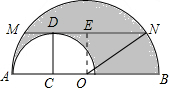 解:如图,作OE⊥MN于E.
解:如图,作OE⊥MN于E.
∵大半圆的弦AB与小半圆相切,
∴CD为⊙C的半径,
∴OC⊥MN,
又MN∥AB,
∴四边形DCOE为矩形,
∴OE=CD,
∵OE⊥MN,
∴ME=NE=
MN=
a,
在Rt△OEN中,ON2-OE2=EN2=
a2,
∵阴影部分的面积=
S⊙C-
S⊙O=
(π•ON2-π•CD2)=
π(ON2-OE2)=
a2.
故答案为:
a2.
 解:如图,作OE⊥MN于E.
解:如图,作OE⊥MN于E.∵大半圆的弦AB与小半圆相切,
∴CD为⊙C的半径,
∴OC⊥MN,
又MN∥AB,
∴四边形DCOE为矩形,
∴OE=CD,
∵OE⊥MN,
∴ME=NE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OEN中,ON2-OE2=EN2=
| 1 |
| 4 |
∵阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 8 |
故答案为:
| π |
| 8 |
点评:本题考查了圆的切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,小纸片中AD∥BC,沿EF对折后使两部分重合,若∠AEF=110°,则∠1=
如图,小纸片中AD∥BC,沿EF对折后使两部分重合,若∠AEF=110°,则∠1=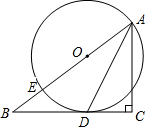 已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,联结AD.
已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,联结AD. 如图所示,在⊙O中,弦AB、CD垂直相交于点E,求证:∠BOC+∠AOD=180°.
如图所示,在⊙O中,弦AB、CD垂直相交于点E,求证:∠BOC+∠AOD=180°.