题目内容
5. 如图,AC是⊙O的直径,∠ACB=90°,CA=CB,连接BO交⊙O于点D,连接AD,则tan∠ADO的值为( )
如图,AC是⊙O的直径,∠ACB=90°,CA=CB,连接BO交⊙O于点D,连接AD,则tan∠ADO的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{2}{3}$ | C. | 3-$\sqrt{5}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
分析 过点D作DE⊥AC于E,根据平行线的性质得:∠ODE=∠OBC,由等角的三角函数列式得:tan∠ODE=$\frac{OE}{ED}$=$\frac{1}{2}$,设OE=x,DE=2x,则OD=OA=$\sqrt{5}$x,表示AE=(1+$\sqrt{5}$)x,由半径相等和等边对等角可得结论.
解答  解:过点D作DE⊥AC于E,
解:过点D作DE⊥AC于E,
∵AC=BC=2OB,
∵∠ACB=∠DEO=90°,
∴BC∥DE,
∴∠ODE=∠OBC,
∴tan∠ODE=tan∠OBC=$\frac{OC}{BC}$=$\frac{OE}{ED}$=$\frac{1}{2}$,
设OE=x,DE=2x,则OD=OA=$\sqrt{5}$x,
∴AE=OA+OE=(1+$\sqrt{5}$)x,
∵OD=OA,
∴tan∠ADO=tan∠DOA=$\frac{DE}{AE}$=$\frac{2x}{(1+\sqrt{5})x}$=$\frac{2}{1+\sqrt{5}}$=$\frac{\sqrt{5}-1}{2}$;
故选A.
点评 本题考查了圆周角定理、三角函数,能做出辅助线,得DE=2OE是关键.

练习册系列答案
相关题目
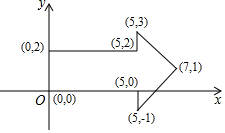 如图,箭头图案是将坐标分别为(0,0),(0,2),(5,2),(5,3),(7,1),(5,-1),(5,0),(0,0)的点用线段依次连接而成的,现把图中的格点分别如下变换:
如图,箭头图案是将坐标分别为(0,0),(0,2),(5,2),(5,3),(7,1),(5,-1),(5,0),(0,0)的点用线段依次连接而成的,现把图中的格点分别如下变换: