题目内容
在△ABC中，三个内角满足∠B-∠A=∠C-∠B，则∠B等于
- A.70°
- B.60°
- C.90°
- D.120°
B
分析：先利用三角形内角和定理可得∠A+∠B+∠C=180°，即∠A+∠C=180°-∠B，再由已知条件可得∠A+∠C=2∠B，两个等式联合，可得关于∠B的方程，解即可．
解答：∵∠B-∠A=∠C-∠B，
∴∠A+∠C=2∠B，
又∵∠A+∠B+∠C=180°，
∴∠A+∠C=180°-∠B，
∴2∠B=180°-∠B，
∴∠B=60°．
故选B．
点评：本题利用了三角形内角和定理以及解一元一次方程的有关知识．
三角形三个内角的和等于180°．
分析：先利用三角形内角和定理可得∠A+∠B+∠C=180°，即∠A+∠C=180°-∠B，再由已知条件可得∠A+∠C=2∠B，两个等式联合，可得关于∠B的方程，解即可．
解答：∵∠B-∠A=∠C-∠B，
∴∠A+∠C=2∠B，
又∵∠A+∠B+∠C=180°，
∴∠A+∠C=180°-∠B，
∴2∠B=180°-∠B，
∴∠B=60°．
故选B．
点评：本题利用了三角形内角和定理以及解一元一次方程的有关知识．
三角形三个内角的和等于180°．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
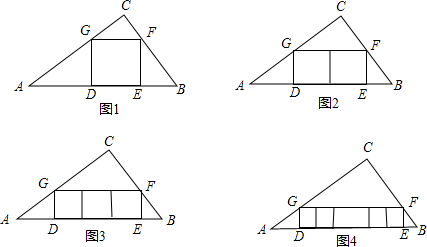
如图，在△ABC中，AB=AC=
（1）如图，若在△ABC中有三个内接正方形，其边长分别为a=7，b=5，c=2．试证明∠ACB为直角．