题目内容
是否有一组勾股数(整数)能构成含有45°角的直角三角形?若有,举出一例,若无,请说明理由.
考点:勾股数,等腰直角三角形
专题:探究型
分析:首先设一条直角边为a,由等腰直角三角形的性质得出另外一条直角边也为a,斜边为
a,由于
是无理数,所以当a为正整数时,
a是无理数;当
a为正整数时,a是无理数;根据勾股数的定义可知不存在任何一组勾股数(整数)能构成含有45°角的直角三角形.
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:不存在任何一组勾股数(整数)能构成含有45°角的直角三角形.理由如下:
设设一条直角边为a,则另外一条直角边也为a,斜边为
a,
∵
是无理数,
∴当a为正整数时,
a是无理数,a、a、
a不是勾股数;
当
a为正整数时,a是无理数,a、a、
a不是勾股数;
故不存在任何一组勾股数(整数)能构成含有45°角的直角三角形.
设设一条直角边为a,则另外一条直角边也为a,斜边为
| 2 |
∵
| 2 |
∴当a为正整数时,
| 2 |
| 2 |
当
| 2 |
| 2 |
故不存在任何一组勾股数(整数)能构成含有45°角的直角三角形.
点评:本题考查了勾股数:满足a2+b2=c2的三个正整数,称为勾股数.同时考查了等腰直角三角形的性质.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图,点P是半径为5的⊙O内一点,且OP=3,在过点P的所有弦中,长度为8的弦有( )
如图,点P是半径为5的⊙O内一点,且OP=3,在过点P的所有弦中,长度为8的弦有( )| A、0条 | B、1条 | C、2条 | D、3条 |
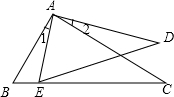 如图∠1=∠2,∠C=∠D,求证:AB•AD=AC•AE.
如图∠1=∠2,∠C=∠D,求证:AB•AD=AC•AE.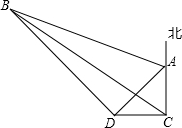 一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号).
一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号).